転移学習（Transfer Learning）

機械学習プロフェッショナルシリーズ

第2章転移学習の基礎

統合資料

2025年4月14日

本資料では、転移学習の基礎的な概念から、具体的な手法や課題までを体系的に解説します。各セクションは独立して理解できるように構成されていますが、全体を通して転移学習の理論的基盤と実践的な応用について理解を深めることができます。

2.1 転移学習の基本問題と目的

本日の内容

転移学習の基本問題
転移学習の目的
従来の機械学習と転移学習の違い
転移学習を成功させるための3つの基本問題
- いつ転移するか（when to transfer）
- 何を転移するか（what to transfer）
- どう転移するか（how to transfer）

転移学習の基本問題

転移学習の基本的な問題意識

3つの基本的な問い

何を（what）転移するか
いつ（when）転移するか
どうやって（how）転移するか

重要な概念

ドメインシフト：ドメインが異なることを数学的に定義した概念
転移仮定：転移が可能となる条件の定式化
不一致度：ドメインのずれの大きさを評価する指標
負転移：ドメインのずれが原因で生じる性能低下

転移学習は異なるドメイン間での知識の転移を扱うため、ドメイン間の関係性を理解することが重要です。本章では、これらの概念を定義し、転移学習の理論的基盤を構築します。

転移学習の目的

転移学習の数学的定義

転移学習の目的は、元ドメイン$\mathbb{D}_S$で獲得した知識を利用して目標ドメイン$\mathbb{D}_T$の期待リスク最小となる仮説を学習すること

期待リスク(復習)

定義1.1（期待リスク）: データ $(\mathbf{X}, Y)$ の従う確率分布 $P_{X,Y}$ のもとでの仮説 $h$ の期待リスク $R(h)$ は、$h$ に対する損失 $\mathcal{L}$ の期待値

$R(h) := \mathbb{E}_{(\mathbf{X}, Y) \sim P_{X,Y}}[ \mathcal{L}(\mathbf{X}, Y; h)] = \mathbb{E}_{(\mathbf{X}, Y) \sim P_{X,Y}}[ \ell(h(\mathbf{X}), Y)]$

元ドメインと目標ドメイン

元ドメイン（Source Domain）：知識獲得の出発点 $\mathbb{D}_S$
目標ドメイン（Target Domain）：知識適用の対象 $\mathbb{D}_T$

ドメイン(復習)

定義1.4（ドメイン）

入力空間 $\mathcal{X}$ と出力空間 $\mathcal{Y}$ の直積空間 $\mathcal{X} \times \mathcal{Y}$ とそのうえで定義された同時分布 $P_{X,Y}$ の組 $\mathbb{D} = (\mathcal{X} \times \mathcal{Y}, P_{X,Y})$ をドメインと呼びます。ここで、$X, Y$ はそれぞれ入力および出力を表す確率変数です。

理想的なケース

もし元ドメインと目標ドメインが完全に一致していれば（$\mathcal{X}_T \times \mathcal{Y}_T = \mathcal{X}_S \times \mathcal{Y}_S$かつ$P^T_{X,Y} = P^S_{X,Y} = P_{X,Y}$）、転移学習の問題は元ドメインを訓練データ、目標ドメインをテストデータとする従来の機械学習の問題として考えることができます。

従来の機械学習と転移学習の違い

従来の機械学習の仮定

訓練データとテストデータが同一の確率分布$P_{X,Y}$から独立に生成されたもの
この仮定のもとで、訓練データ（元ドメイン）の経験リスク最小化で得られた仮説がテストデータ（目標ドメイン）に汎化することが正当化される

転移学習の前提

一般に元ドメインは目標ドメインと類似しているが異なると考える
数学的に以下の状況を考えることに相当：
- $P^T_{X,Y} \neq P^S_{X,Y}$（同質的ドメインシフト）
- または $\mathcal{X}_T \times \mathcal{Y}_T \neq \mathcal{X}_S \times \mathcal{Y}_S$（異質的ドメインシフト）

転移学習では、元ドメインと目標ドメインのデータが同一分布からのサンプルではないため、単純に元ドメインで学習したモデルが目標ドメインでも機能するとは限りません。

転移学習を成功させるための3つの基本問題

いつ転移するか
- 転移を成功させるために元ドメインと目標ドメインがどのような性質を満たしている必要があるか
- 似ているドメイン、似ていないドメインの定量的な区別
- 転移学習が失敗するケースの特定
何を転移するか
- どのような知識を転移するのか
- 転移に適した知識の種類の特定
どう転移するか
- どのように転移を実現するのか
- 具体的なアルゴリズムの設計

本章では特に「いつ転移するか」と「何を転移するか」を説明し、具体的なアルゴリズムを議論する「どう転移するか」は次章以降で説明します。

2.2 いつ転移するか

いつ転移するか（when to transfer）

基本問題

いつ転移するか（when to transfer）は、転移学習がどのような状況であれば成功するのかを掘り下げる問題です。具体的には、以下の点を検討します：

ドメインが似ている、あるいは似ていないとはどういうことか
転移学習が失敗するとはどういうことか
どのような状況で転移学習が失敗しうるか

「いつ転移するか」という問題は、転移学習を実践する際の重要な判断基準となります。元ドメインと目標ドメインの関係性によって、転移学習が有効かどうか、どのような方法が適切かが決まります。

2.2.1 ドメインシフトと転移仮定

ドメインシフトの概念

ドメインシフト（Domain Shift）とは

元ドメイン（source domain）と目標ドメイン（target domain）の間の差異
通常の機械学習では、訓練データとテストデータが同一分布からサンプリングされることを仮定
転移学習では、この仮定を緩和し、ドメイン間での知識転移を考える

ドメインシフトの形式的定義

元ドメイン $\mathbb{D}_S = (\mathcal{X}_S \times \mathcal{Y}_S, P_{X,Y}^S)$ と目標ドメイン $\mathbb{D}_T = (\mathcal{X}_T \times \mathcal{Y}_T, P_{X,Y}^T)$ の差を「ドメインシフト」と呼びます。

ドメインシフトの種類

2種類の基本的なドメインシフトが存在する：
- 同質的ドメインシフト（homogeneous domain shift）
- 異質的ドメインシフト（heterogeneous domain shift）
これらは転移学習で扱う問題の性質を大きく左右する

ドメインシフトの種類によって、転移学習の難しさと適切なアプローチが変わります。同質的か異質的かという基本的な区別が、転移学習手法選択の第一歩となります。

同質的ドメインシフトと異質的ドメインシフト

同質的ドメインシフト（Homogeneous Domain Shift）

$\mathcal{X}_T \times \mathcal{Y}_T = \mathcal{X}_S \times \mathcal{Y}_S$ かつ $P_{X,Y}^T \neq P_{X,Y}^S$

すなわち、データのサンプル空間は元ドメインと目標ドメインで共通であり、両ドメインの違いはデータ生成分布のみである状況

データセットシフト（dataset shift）とも呼ばれる
例：同じカメラで撮影した屋内画像と屋外画像
分布シフト（distribution shift）と呼ぶこともある
さらに特定のタイプのシフトに細分化される：
- 共変量シフト（covariate shift）
- クラス事前確率シフト（class prior shift）
- サンプル選択バイアス（sample selection bias）など

同質的ドメインシフトは、転移学習の中でも比較的扱いやすい問題設定です。データの表現形式は同じで、分布のみが異なるため、既存の特徴表現を活用しやすいという特徴があります。

同質的ドメインシフトと異質的ドメインシフト（続き）

異質的ドメインシフト（Heterogeneous Domain Shift）

$\mathcal{X}_T \times \mathcal{Y}_T \neq \mathcal{X}_S \times \mathcal{Y}_S$

すなわち、サンプル空間が元ドメインと目標ドメインで異なる場合を扱う

入力特徴や出力ラベルの次元や意味が異なる
例：
- テキスト情報から画像情報への転移（クロスモーダル転移）
- 異なる解像度の画像間での転移
- 異なる言語間での自然言語処理タスクの転移
同質的ドメインシフトよりも難しい問題設定
特徴空間の変換や共通表現の学習が必要

異質的ドメインシフトでは、サンプル空間が異なるため、元ドメインと目標ドメインを単純に比較できません。この場合、両ドメインに共通する特徴空間を見つけるアプローチが重要になります。深層表現学習の発展により、この分野は大きく進展しています。

極端なケース：ドメイン一致

転移学習の最も極端なケース

$\mathbb{D}_S = \mathbb{D}_T$

元ドメインと目標ドメインが完全に一致している状況
この場合は通常の機械学習と同等になる
転移学習の特別な技術は不要

これは理論的な極限ケースであり、実際の応用では完全な一致はまれです。しかし、この極限ケースを理解することで、転移学習の理論的基盤を把握できます。

なぜこの場合は単なる機械学習と同等か

両ドメインのデータが同じ確率分布に従っている
元ドメインで学習したモデルは、そのまま目標ドメインで最適な性能を発揮できる
追加の転移テクニックは必要ない

近似的ドメイン類似性

現実的なシナリオ

$\mathbb{D}_S \approx \mathbb{D}_T$

元ドメインと目標ドメインが適当な指標のもとで近い場合
このとき、元ドメインから目標ドメインへの知識転移が成功する可能性が高い

「近さ」の概念

ドメイン間の「近さ」は様々な方法で定義可能
同質的ドメインシフトの場合：
- 確率分布間の距離（KLダイバージェンス、Wasserstein距離など）
- 経験的確率分布の差異（最大平均差異など）
異質的ドメインシフトの場合：
- 共通特徴空間での表現の類似性
- 特徴抽出関数の対応関係

実際の応用では、多くの場合、元ドメインと目標ドメインは完全には一致しませんが、ある程度の類似性があります。同質的か異質的かによって「近さ」の定義方法が異なり、それに応じて転移手法も変わってきます。

転移仮定の必要性

一般的な状況の課題

現実では $\mathbb{D}_S$ と $\mathbb{D}_T$ が近いことは保証されない
転移学習は「ドメイン間に何らかの関係性がある」という前提に基づく
この関係性についての仮説を転移仮定（transfer assumption）と呼ぶ

転移仮定の役割

転移仮定は、元ドメインと目標ドメインの間に存在する特定の関係性を定式化するものです。この仮定により、元ドメインで学習した知識を目標ドメインに転用する方法が決まります。

同質的ドメインシフトでの転移仮定例

共変量シフト: 入力の周辺分布は変化するが、条件付き分布は同じ
クラス事前確率シフト: 出力の周辺分布は変化するが、条件付き分布は同じ
サンプル選択バイアス: 目標ドメインのデータは元ドメインのデータの部分集合

転移仮定の必要性（続き）

異質的ドメインシフトでの転移仮定例

特徴空間変換: $f_S : \mathcal{X}_S \to \mathcal{Z}$ と $f_T : \mathcal{X}_T \to \mathcal{Z}$ が存在し、共通特徴空間 $\mathcal{Z}$ 上で同質的ドメインシフトの転移仮定が成立
特徴対応: 元ドメインの特徴と目標ドメインの特徴間に対応関係が存在
特徴分解: 両ドメインの特徴がドメイン固有部分とドメイン不変部分に分解可能

表現学習の役割

深層ニューラルネットワークによる表現学習の性能向上により、異質的ドメインシフトへの対応が飛躍的に向上
特に深層モデルを用いた異質的ドメインシフトへの対応は現在の転移学習における主流の方法の一つ

異質的ドメインシフトは、同質的ドメインシフトに比べて難しい問題ですが、表現学習の進歩により大きく発展している分野です。両ドメインに共通する潜在空間を見つけることが鍵となります。

転移学習の成功条件

転移学習が成功するための条件

理想的な条件

完全ドメイン一致: $\mathbb{D}_S = \mathbb{D}_T$
近似的ドメイン一致: $\mathbb{D}_S \approx \mathbb{D}_T$

現実的な条件

適切な転移仮定が存在する
その仮定を活用した転移手法が利用可能

同質的・異質的ドメインシフトでの成功条件の違い

同質的ドメインシフトの場合:
- 分布の差異が小さいか、特定のパターンに従っている
- 共変量シフトやクラス事前確率シフトなどの仮定が成立
異質的ドメインシフトの場合:
- 効果的な共通特徴空間が存在する
- 特徴変換関数が学習可能である

転移学習の成功は、適切な転移仮定の選択と、それに基づく効果的な転移手法の適用にかかっています。仮定が現実と合致しない場合、転移は失敗する可能性が高くなります。

転移学習の成功条件（続き）

転移仮定の選択における考慮事項

問題設定や観測されたデータの性質
ドメインが同質的か異質的かの判断
ドメインに関する先見的な知識
どのような転移仮定が妥当かを慎重に見極める必要がある

転移方法の適切な選択

転移仮定に基づいて適切な転移学習方法を選択
同質的ドメインシフトの場合:
- インスタンス重み付け法（共変量シフト仮定）
- クラス比率調整法（クラス事前確率シフト仮定）
異質的ドメインシフトの場合:
- 表現学習による共通特徴空間の発見
- ドメイン対応付け（domain mapping）技術

適切な転移仮定と転移手法の選択は、問題の性質と利用可能なデータに強く依存します。複数の手法を試し、検証データで評価することが実践的なアプローチです。

まとめ: ドメインシフトと転移仮定

本節の重要ポイント

転移学習の成功条件はドメイン間の関係性に大きく依存する
ドメインシフトには同質的と異質的の2種類がある
- 同質的: サンプル空間は同じだが分布が異なる
- 異質的: サンプル空間自体が異なる
極端なケース（$\mathbb{D}_S = \mathbb{D}_T$）では通常の機械学習と同等
ドメインが近似的に一致（$\mathbb{D}_S \approx \mathbb{D}_T$）する場合、転移は成功しやすい
一般的には、ドメインシフトのタイプに応じた適切な転移仮定の選択が鍵となる
異質的ドメインシフトでは特に、共通特徴空間の発見が重要な課題となる

2.2.1節で学んだドメインシフトと転移仮定の概念は、以降の章で紹介される様々な転移学習手法の理論的基盤となります。同質的・異質的ドメインシフトの区別と、それぞれに適した転移仮定の選択が、効果的な転移学習の鍵です。

2.2.2 確率分布間の距離測度に基づく不一致度

ドメインの不一致度とその重要性

転移学習における前提

転移学習では、元ドメインと目標ドメインの分布が異なることを前提
転移仮定（例えば共変量シフト）は、分布の一致している部分と異なる部分を明示
しかし、転移仮定からはどの程度異なるかは分からない

不一致度（Discrepancy）の必要性

ドメイン間の分布のずれを定量的に評価するための概念
主に二つのアプローチ：
- 確率密度比に基づく手法
- 確率分布間の距離尺度に基づく手法

分布の不一致度は理論的に重要なだけでなく、実用的なアルゴリズムの設計にも直接関わります。分布のずれが大きいほど転移が難しくなり、ドメイン適応のために特別な工夫が必要になります。

確率密度比の概念

確率密度比（Density Ratio）の定義

確率密度比 $r(x)$ は、目標ドメインの確率密度関数 $p^T(x)$ と元ドメインの確率密度関数 $p^S(x)$ の比として定義されます：

$r(x) = \frac{p^T(x)}{p^S(x)}$ (2.5)

確率密度比の特性

$p^T(x) = p^S(x)$ のとき、すべての $x$ で $r(x) = 1$
$p^T(x) \neq p^S(x)$ のとき、入力 $x$ が目標ドメインの分布からの事例らしいほど $r(x)$ の値は大きくなる
元ドメインのデータ $x_1^S, ..., x_{n_S}^S$ に対して密度比 $r(x_i^S)$ を評価すれば、その値の大小によって目標ドメインとの近さを見積もることが可能

課題

確率密度関数 $p^T(x)$ および $p^S(x)$ は一般に未知
密度比 $r(x_i^S)$ の値は観測データから推定する必要がある

確率密度比の概念（続き）

密度比の推定方法

素朴な方法：$p^T(x)$ および $p^S(x)$ を個別に推定してそれらの比をとる
しかし、それぞれの推定誤差が比をとる操作によって増大する可能性がある
一般に高精度は望めない

直接推定アプローチ

密度比 $r(x)$ をデータから直接推定する手法が開発されている
代表的な密度比推定のアプローチ：
- 密度比関数 $r(x)$ に対して線形基底関数モデルを仮定
- $\hat{r}(x; \alpha) = \alpha^\top \varphi(x) = \sum_{l=1}^L \alpha_l \varphi_l(x)$ (2.6)
- 真の密度比 $r(x)$ との誤差を最小化してモデルパラメータ $\alpha$ を推定

式(2.6)において、$\varphi(x) = (\varphi_1(x), ..., \varphi_L(x))^\top$ は入力 $x$ に対する基底関数ベクトルを表します。基底関数としては、例えば目標ドメインの入力データを参照点として用いたガウスカーネルなどがよく用いられます。

密度比推定手法

密度比推定の主要手法

1. カルバック・ライブラー重要度推定法（KLIEP）

目標ドメインの確率密度関数を密度比モデルを用いて $\hat{p}^T(x) = \hat{r}(x; \alpha)p^S(x)$ と表し、真の確率密度関数とのカルバック・ライブラーダイバージェンス
$D_{\mathrm{KL}}(p^T(x) \parallel \hat{p}^T(x)) = \int p^T(x) \log \frac{p^T(x)}{\hat{r}(x; \alpha)p^S(x)} dx$
を最小化して $\alpha$ を推定するカルバック・ライブラー重要度推定法（Kullback-Leibler importance estimation procedure, KLIEP）がある
ここで、(2.7) の2行目の第1項はモデルパラメータを含んでいないため、最適化においては定数となることに注意
よって、KLIEP の目的関数は第2項を観測データによって近似した
$\int p^T(x) \log \hat{r}(x; \alpha) dx \approx \frac{1}{n_T} \sum_{i=1}^{n_T} \log \hat{r}(x_i^T; \alpha)$ (2.8)
となる

密度比推定手法（続き）

2. 制約なし最小二乗重要度適合法（uLSIF）

密度比推定のもう一つの主要なアプローチに制約なし最小二乗重要度適合法（unconstrained least-squares importance fitting, uLSIF）がある
この方法では、密度比モデル $\hat{r}(x; \alpha)$ と真の密度比 $r(x)$ の二乗誤差
$\frac{1}{2} \int (\hat{r}(x; \alpha) - r(x))^2 p^S(x) dx$

$= \frac{1}{2} \int \hat{r}(x; \alpha)^2 p^S(x) dx - \int \hat{r}(x; \alpha) p^T(x) dx + \frac{1}{2} \int r(x) p^T(x) dx$ (2.9)
を直接最小化してパラメータ $\alpha$ を推定する
(2.9) において、2行目の第3項はパラメータを含まないため最適化においては定数となっている
したがって、第1項と第2項をそれぞれ観測データで近似した
$\frac{1}{2n_S} \sum_{i=1}^{n_S} \hat{r}(x_i^S; \alpha)^2 - \frac{1}{n_T} \sum_{i=1}^{n_T} \hat{r}(x_i^T; \alpha) + \frac{\lambda}{2} \|\alpha\|_2^2$ (2.10)
を最小化してパラメータを推定する

(2.10) の第3項は $\lambda \geq 0$ を正則化パラメータとする正則化項です。(2.10) に密度比の線形基底関数モデル (2.6) を代入し、パラメータ $\alpha$ に関する2次形式の形に整理すると、最適解が解析的に求まります。

f-ダイバージェンス

f-ダイバージェンスの定義

定義2.1（f-ダイバージェンス）

$\mathbb{R}_{\geq 0}$ を非負の実数全体とし、$\phi : \mathbb{R}_{\geq 0} \to \mathbb{R}$ を凸かつ下半連続で $\phi(1) = 0$ を満たすような関数とします。このとき、二つの確率分布 $P_X^T$ と $P_X^S$ の間の f-ダイバージェンス $D_\phi(P_X^S \parallel P_X^T)$ は、

$D_\phi(P_X^S \parallel P_X^T) = \int p^T(x) \phi \left( \frac{p^S(x)}{p^T(x)} \right) dx$ (2.13)

で定義されます。

f-ダイバージェンスの特性

$\phi$ が凸関数であることから、イェンセンの不等式によって
$D_\phi(P_X^S \parallel P_X^T) \geq \phi \left( \int p^T(x) \frac{p^S(x)}{p^T(x)} dx \right) = \phi(1) = 0$
f-ダイバージェンスは非負性を持つ
f-ダイバージェンスは以下のような変分下界を持つ
$D_\phi(P_X^S \parallel P_X^T) \geq \sup_{g \in \mathcal{G}} [\mathbb{E}_{x \sim P_X^S}[g(x)] - \mathbb{E}_{x \sim P_X^T}[\phi^*(g(x))]]$ (2.14)
- $\phi^*(y) = \sup_{x \in \mathbb{R}_{\geq 0}} \{xy - \phi(x)\}$ は $\phi$ のフェンシェル共役関数(ルジャンドル変換の拡張)
- $\mathcal{G}$ は $\mathcal{X}$ から $\text{dom}(\phi^*)$ への関数全体

f-ダイバージェンス（続き）

代表的なf-ダイバージェンス

関数 $\phi$ の取り方によってさまざまなダイバージェンスを表現できます。

名称	$\phi(x)$	特徴
カルバック・ライブラーダイバージェンス	$x \log x$	情報理論的解釈が可能、確率分布の情報量の差
イェンセン・シャノンダイバージェンス	$-(x+1)\log \frac{1+x}{2} + x \log x$	対称的な尺度、$P_X^S$ と $P_X^T$ の役割を入れ替えても値は変わらない
全変動距離	$\frac{1}{2}\|x-1\|$	直感的に解釈しやすい、分布間の最大確率差

下界表現による推定

式(2.14)の下界表現によって、データから f-ダイバージェンスを推定する問題を下界の最大化問題、すなわち変分推論問題とみなして解くことも可能

H-ダイバージェンス

H-ダイバージェンスの定義

定義2.2（H-ダイバージェンス）

二つの確率分布 $P_X^T$ と $P_X^S$ の間の $\mathcal{H}$-ダイバージェンス $D_{\mathcal{H}\triangle\mathcal{H}}(P_X^S, P_X^T)$ は、

$D_{\mathcal{H}\triangle\mathcal{H}}(P_X^S, P_X^T) = 2 \sup_{h \in \mathcal{H}} \left| P_X^S(I_h) - P_X^T(I_h) \right|$ (2.17)

で定義されます。ここで、$I_h = \{x \in \mathcal{X} | h(x) = 1\}$ とおきました。

H-ダイバージェンスの解釈

目標ドメインと元ドメインで同じ仮説を用いたときにラベルが1と予測される入力集合を考え、その確率の差を評価
もっとも差のある仮説を選択した時の確率の差(の2倍)
定義から、$D_{\mathcal{H}\triangle\mathcal{H}}(P_X^S, P_X^T)$ は以下のように等価な変形が可能

$D_{\mathcal{H}\triangle\mathcal{H}}(P_X^S, P_X^T) = 2 \sup_{h \in \mathcal{H}} \left| R_S(h, 1) - R_T(h, 1) \right|$ (2.18)

$= 2 \sup_{h \in \mathcal{H}} \left| 1 - (R_S(h, 0) + R_T(h, 1)) \right|$

ここで、$R_S(h, a) = \mathbb{E}_{x \sim P_X^S}[|h(x) - a|]$, $R_T(h, a) = \mathbb{E}_{x \sim P_X^T}[|h(x) - a|]$ としています。

H-ダイバージェンス（続き）

H-ダイバージェンスの特性

$\mathcal{H}$が対称な仮説集合のとき、すなわち $h \in \mathcal{H}$ならば $1 - h \in \mathcal{H}$が成り立つとき、観測データに基づく経験的な$\mathcal{H}$-ダイバージェンスを以下のように表現できます

$\hat{D}_{\mathcal{H}\triangle\mathcal{H}}(P_X^S, P_X^T) = 2 \left( 1 - \min_{h \in \mathcal{H}} \left( \frac{1}{n_S} \sum_{i=1}^{n_S} \mathbb{I}[h(x_i^S) \neq 0] + \frac{1}{n_T} \sum_{i=1}^{n_T} \mathbb{I}[h(x_i^T) \neq 1] \right) \right)$ (2.19)

ここで、$\mathbb{I}[A]$ は $A$ が真のとき 1 を、$A$ が偽のとき 0 を返す指示関数です。

解釈とドメイン識別問題

(2.19) の min 以降の項は、仮説 $h$ が元ドメインの入力に対するラベルをすべて 0 と予測し、目標ドメインの入力に対するラベルをすべて 1 と予測すれば 0 となる
そうではない仮説を用いた場合、この項は 0 より大きな値を持ち、$\mathcal{H}$-ダイバージェンスはより小さくなる
$\mathcal{H}$-ダイバージェンスは $\mathcal{H}$ の仮説が元ドメインの入力と目標ドメインの入力をどれくらい見分けられるかという観点で $P_X^S$ と $P_X^T$ の類似度を評価していると解釈できる

最大平均不一致度（MMD）

再生核ヒルベルト空間

定義2.3（再生核ヒルベルト空間）

$\mathcal{F}$ を $\mathcal{X}$ 上の関数 $f : \mathcal{X} \to \mathbb{R}$ を要素に持つヒルベルト空間とし、その内積を $\langle \cdot, \cdot \rangle_{\mathcal{F}}$ で表すとします。ある関数 $k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}$ が存在して (1) 任意の $x \in \mathcal{X}$ に対して $\phi_x = k(x, \cdot) \in \mathcal{F}$, (2) 任意の $f \in \mathcal{F}$ と $x \in \mathcal{X}$ に対して $f(x) = \langle f, \phi_x \rangle_{\mathcal{F}}$ が成り立つとき、$\mathcal{F}$ を $k$ を再生核に持つ再生核ヒルベルト空間と呼びます。

最大平均不一致度（MMD）の定義

定義2.4（最大平均不一致度 (MMD)）

$\mathcal{F}$ を関数 $f : \mathcal{X} \to \mathbb{R}$ のなす再生核ヒルベルト空間とします。このとき、$P_X^T$ と $P_X^S$ の間の MMD は

$D_{\text{MMD}}(P_X^S, P_X^T) = \sup_{f \in \mathcal{F}} \left| \mathbb{E}_{x^S \sim P_X^S}[f(x^S)] - \mathbb{E}_{x^T \sim P_X^T}[f(x^T)] \right|$ (2.20)

で定義されます。

すなわち、二つのドメインの分布の近さを、それぞれのドメインにおけるある関数の値の期待値の差で評価するのが MMD です。

最大平均不一致度（MMD）（続き）

MMDの理論的特性

補題2.5

$P_X^T$, $P_X^S$ は距離空間 $\mathcal{X}$ 上のボレル確率測度とします。このとき、$P_X^T = P_X^S$ であることの必要十分な条件は、

$\mathbb{E}_{x^S \sim P_X^S}[f(x^S)] = \mathbb{E}_{x^T \sim P_X^T}[f(x^T)]$

が任意の有界な可測かつ可積分関数 $f : \mathcal{X} \to \mathbb{R}$ に対し成り立つことです。

補題2.5より、$P_X^T = P_X^S$ を帰無仮説、$P_X^T \neq P_X^S$ を対立仮説とする二標本検定を考えるとき、MMD は帰無仮説の必要十分条件が正しいかどうかを評価する指標であると解釈できます。すなわち、MMD をこの仮説検定の検定統計量として用いることができます。

MMD の経験的推定

観測データから MMD を推定する式：

$\hat{D}_{\text{MMD}}(P_X^S, P_X^T) = \sup_{f \in \mathcal{F}} \left( \frac{1}{n_S} \sum_{i=1}^{n_S} f(x_i^S) - \frac{1}{n_T} \sum_{i=1}^{n_T} f(x_i^T) \right)$ (2.21)

最適輸送理論

最適輸送理論の概要

最適輸送理論は「ある場所で採掘した土を別の場所で工事に用いるとき、輸送コストを最小にする輸送方法を求めよ」という問題が、モンジュによって数学的に定式化されたところから始まったとされる
元ドメインの分布 $P_X^S$ と目標ドメインの分布 $P_X^T$ に対して、
$\tau_{\#}P_X^S = P_X^T$ を満たす可測関数 $\tau : \mathcal{X} \to \mathcal{X}$
の中で輸送コスト
$\int_{\mathcal{X}} \|x - \tau(x)\| dP_X^S$ (2.22)
が最小となるものを求める問題として定式化できる

輸送写像

ここで、$\tau_{\#}P_X^S$ は関数 $\tau$ による分布 $P_X^S$ の押し出しと呼ばれるもので、$A \subset \mathcal{X}$ に対して $\tau_{\#}P_X^S(A) = P_X^S(\tau^{-1}(A))$ で定義される
この条件は、目標ドメインの地点 $A$ で受け取る土の量は、$A$ に土を送る元ドメインの地点 $\tau^{-1}(A)$ から運び出す土の量 $P_X^S(\tau^{-1}(A))$ と等しいことを要請するものである
これにより輸送の前後で土の量が変わらない（すなわち密度の総和が 1 であるという確率分布の性質が保たれる）ことが保証される

ワッサースタイン距離

最適輸送理論の背景

最適輸送理論は「ある場所で採掘した土を別の場所で工事に用いるとき、輸送コストを最小にする輸送方法を求めよ」という問題がモンジュによって数学的に定式化されたところから始まった
転移学習の文脈では、元ドメインの分布 $P_X^S$ と目標ドメインの分布 $P_X^T$ に対して、$\tau_{\#}P_X^S = P_X^T$ を満たす可測関数 $\tau : \mathcal{X} \to \mathcal{X}$ の中で輸送コスト
$\int_{\mathcal{X}} \|x - \tau(x)\| dP_X^S$ (2.22)
が最小となるものを求める問題として定式化できる

カップリングとは

$\pi$ が $P_X^S$ と $P_X^T$ のカップリングであるとは、射影関数 $\mathrm{proj}_i(x_1, x_2) = x_i$, $i = 1, 2$ に対して $(\mathrm{proj}_1)_{\#}\pi = P_X^S$, $(\mathrm{proj}_2)_{\#}\pi = P_X^T$ が満たされることと定義される
機械学習の研究では、コスト関数の指数 $p$ が $1$ として考察されることが特に多い
これは、$p = 1$ のとき (2.23) の最小化問題が線形計画問題として書き下せるという事実や、後述するカントロヴィッチ・ルービンスタイン双対性が利用できるなどの利点があるから

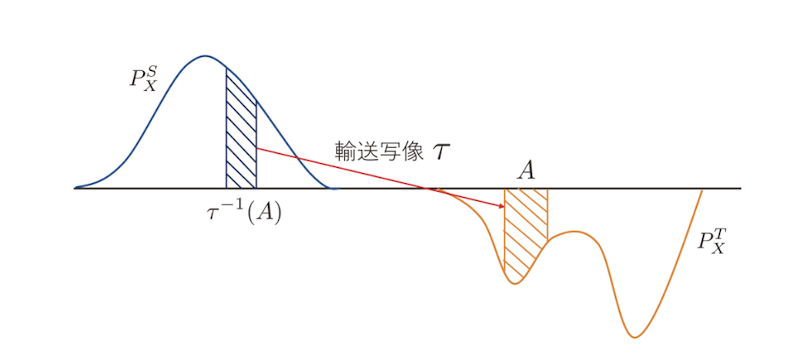
図2.1 モンジュによる最適輸送問題のイメージ

ワッサースタイン距離（続き）

ワッサースタイン距離の定義

定義2.6（ワッサースタイン距離）

元ドメインの分布 $P_X^S$ と目標ドメインの分布 $P_X^T$ の間の $p$ 次ワッサースタイン距離は

$D_{W,p}(P_X^S, P_X^T) = \inf_{\pi \in \Pi(P_X^S, P_X^T)} \left( \int \|x - x'\|^p d\pi(x, x') \right)^{1/p}$ (2.24)

で定義されます。ここで、$\Pi(P_X^S, P_X^T)$ は $P_X^S$ と $P_X^T$ のカップリングの集合です。

ワッサースタイン距離の解釈

ワッサースタイン距離は $P_X^S$ と $P_X^T$ の間に引かれた最短線の長さを表すものと解釈でき、その観点で二つのドメインの近さを評価する
特に $p = 1$ のとき、$D_{W,1}$ を $D_W$ とも記し、次のカントロヴィッチ・ルービンスタイン双対性（Kantorovich-Rubinstein duality）を満たす

$D_W(P_X^S, P_X^T) = \sup_{\varphi \in 1-\mathrm{Lip}} \left( \mathbb{E}_{x \sim P_X^S}[\varphi(x)] - \mathbb{E}_{x \sim P_X^T}[\varphi(x)] \right)$ (2.25)

ここで、1-Lip はリプシッツ定数が 1 であるようなリプシッツ連続な関数の集合を表します。

ワッサースタイン距離（続き）

ワッサースタイン距離の経験的推定

観測データを用いたワッサースタイン距離の経験的推定式：

$\frac{1}{n_S} \sum_{i=1}^{n_S} \varphi(x_i^S) - \frac{1}{n_T} \sum_{i=1}^{n_T} \varphi(x_i^T)$ (2.26)

ワッサースタイン距離と敵対的学習

ワッサースタイン距離の (2.25) や (2.26) による表現は敵対的学習と非常に相性がよく、例えば4.4節で説明するワッサースタイン距離に基づく敵対的表現学習では、$\varphi$ として深層ニューラルネットワークを用いたカントロヴィッチ - ルービンスタイン双対性によって学習問題が定式化される
また、敵対的生成ネットワークの一つであるワッサースタイン GAN の目的関数もカントロヴィッチ - ルービンスタイン双対性に基づいて定式化されたものである

ワッサースタイン距離は、分布間の幾何学的な距離を測る自然な方法を提供するため、特に生成モデルや分布マッチングの応用において重要な役割を果たしています。

まとめ - 確率分布間の距離尺度

転移学習における重要性

転移学習では、元ドメインと目標ドメインの分布の差異を定量的に評価することが理論の基礎
これらの距離尺度は理論的性質だけでなく、実際のアルゴリズム設計にも直結

主要な距離尺度の比較

距離尺度	主な特徴	応用例
f-ダイバージェンス	確率密度比に基づく評価、様々な具体形がある	GANなどの生成モデル
H-ダイバージェンス	ドメイン識別問題と関連	理論的汎化誤差境界、ドメイン不変表現学習
MMD	再生核ヒルベルト空間での平均埋め込みの差	二標本検定、ドメイン適応
ワッサースタイン距離	幾何学的な距離の観点、最適輸送理論に基づく	WGAN、敵対的表現学習

今後の発展方向

計算効率のよい距離尺度の推定法
特定の応用ドメインに適した距離尺度の開発
深層学習と組み合わせた効率的なアルゴリズム

2.2.3 負転移

2.2.3 負転移（Negative Transfer）

負転移とは

転移学習において、元ドメインからの知識転移が逆効果となる現象
目標ドメインでの性能が、転移を行わない場合よりも低下する
転移学習の重要な課題の一つ

負転移の数学的定義

定義2.7（負転移）

どんなアルゴリズム $A$ (ドメインから仮説 $h$ を返す関数/手続き)に対しても

$R_T(A(\mathbb{D}_S, \mathbb{D}_T)) > \min\{R_T(A(\emptyset, \mathbb{D}_T)), R_T(A(\mathbb{D}_S, \emptyset))\}$

が成り立つ時、ドメイン間の負転移が起きているという。

ただし実質的には次を考えれば十分か？

$R_T(A(\mathbb{D}_S, \mathbb{D}_T)) > R_T(A(\emptyset, \mathbb{D}_T))$

$R_T$：目標ドメインでの期待リスク
$A(\mathbb{D}_S, \mathbb{D}_T)$：元ドメインの知識を利用した学習アルゴリズム
$A(\emptyset, \mathbb{D}_T)$：元ドメインの知識を利用しない学習アルゴリズム
$A(\mathbb{D}_S, \emptyset)$：元ドメインの知識のみを利用した学習アルゴリズム

負転移は、元ドメインと目標ドメインの関係性が適切でない場合に発生します。転移学習を実践する際には、負転移の可能性を常に考慮する必要があります。

2.2.3 負転移（続き）

負転移の主な原因

ドメイン間の不一致
- 元ドメインと目標ドメインの分布が大きく異なる
- ドメイン間の距離測度が大きい
不適切な転移仮定
- ドメイン間の関係性に関する仮定が現実と合致しない
- 転移仮定が強すぎる、または弱すぎる
転移手法の選択ミス
- 問題設定に適していない転移手法の選択
- パラメータ設定の不適切さ

負転移の具体例

異なる医療施設間での診断モデルの転移
- 患者の背景や測定方法が大きく異なる場合
- 疾患の特徴が施設によって異なる場合
異なる言語間での自然言語処理モデルの転移
- 言語構造が大きく異なる場合
- 文化的背景が異なる場合

2.2.3 負転移（続き）

負転移の防止策

ドメイン間の関係性の事前評価
- 分布間の距離測度による定量的評価
- ドメイン間の類似性の可視化
適切な転移仮定の選択
- 問題設定に応じた転移仮定の検討
- 複数の転移仮定の比較検討
転移手法の慎重な選択
- 問題設定に適した手法の選択
- パラメータの慎重な調整

実践的なアプローチ

段階的な転移の実施
- 小規模なデータでの事前検証
- 徐々に転移の範囲を拡大
転移の効果の継続的なモニタリング
- 性能指標の定期的な評価
- 必要に応じた転移手法の調整

負転移を完全に防ぐことは難しいですが、適切な事前評価と慎重な実装により、そのリスクを大幅に低減することができます。転移学習を実践する際には、常に負転移の可能性を念頭に置き、段階的なアプローチを取ることが重要です。

2.3 何を転移するか

「何を転移するか」の問題

転移学習における基本問題

「何を転移するか」（what to transfer）は、元ドメインから目標ドメインへ転移する知識として何を用いるかを決定する問題
転移する知識の種類によって、利用可能な問題設定や転移の実現方法が変わる
「いつ転移するか」とあわせて注意深く考慮する必要がある

転移学習の性能指標

$R_T(A(\mathbb{D}_S, \mathbb{D}_T)) \leq \min\{R_T(A(\emptyset, \mathbb{D}_T)), R_T(A(\mathbb{D}_S, \emptyset))\}$

負転移：上記の不等式が成り立たない状況（転移によってリスクが増大）
適切な転移方法の選択は負転移を防ぎ、転移学習を成功させる鍵

転移学習の成功には、ドメイン間の関係性を正確に把握し、それに適した転移方法を選択することが不可欠です。本節では3つの主要な転移方法について詳しく見ていきます。

2.3.1 事例転移（Instance Transfer）

事例転移の基本概念

事例転移は元ドメインのラベル付きデータを目標ドメインへ直接転移するアプローチ
最も直接的な知識転移の形態
前提条件：元ドメインと目標ドメインがよく似ている（$\mathbb{D}_S \approx \mathbb{D}_T$）

事例転移の方法

元ドメインのデータ $\mathbb{D}_S$ を目標ドメインのデータ $\mathbb{D}_T$ と単純に結合
結合後のデータ $\mathbb{D}=\mathbb{D}_S \cup \mathbb{D}_T$ を単一のドメインとみなす
通常の教師あり学習問題として扱う

事例転移は概念的にシンプルですが、ドメイン間の分布の違いが大きい場合、単純な結合では効果的な転移ができない場合があります。そのため、適切な重み付けやデータ選択が必要になることもあります。

2.3.2 特徴転移（Feature Transfer）

特徴転移の基本概念

特徴転移は、表現学習によってデータから抽出した特徴量を用いて元ドメインから目標ドメインへの知識転移を行うアプローチ
事例転移と比較した主な利点：より柔軟なドメイン間の接続が可能

事例転移と特徴転移の違い

事例転移：元ドメインと目標ドメインが空間的に同質（$\mathcal{X}_S\times \mathcal{Y}_S = \mathcal{X}_T\times \mathcal{Y}_T$）のときにのみ実行可能
特徴転移：入力空間$\mathcal{X}_S$と$\mathcal{X}_T$の次元が異なるような空間的に異質な場合にも適用可能

特徴転移は、異なるデータ構造や次元を持つドメイン間で知識を転移する必要がある場合に特に有効です。例えば、異なるセンサーからのデータや、異なる表現形式のデータ間での転移に適しています。

2.3.3 パラメータ転移（Parameter Transfer）

パラメータ転移の基本概念

パラメータ転移は、元ドメインで訓練した機械学習モデルのパラメータを目標ドメインに転移するアプローチ
転移対象となる機械学習モデルの例：
- 回帰モデルや分類モデルなどの予測器
- 特徴抽出器
- 辞書学習によって得られた辞書行列
適用範囲：モデルの種類を切り替えることで、同質的・異質的どちらのドメインシフトの設定でも実行可能

深層学習の普及により、パラメータ転移は現在の転移学習の主流となっています。特に、大規模なモデルを事前学習し、そのパラメータを目標タスクに合わせて微調整する「事前学習+微調整」のアプローチが広く用いられています。

2.3.3 パラメータ転移（続き）

パラメータ転移の主な利点

データプライバシーの保護
- 生データや特徴量を複数のドメインで共有することなくモデルの学習が可能
- プライバシー保護などデータの秘匿性が要請される領域で特に有効
事前学習済みモデルの活用
- 深層学習の発展によって様々な事前学習済みモデルが開発・整備
- 容易に実行可能になったことが普及の要因

現在の主流

これらの利点により、パラメータ転移は現在の転移学習の主流な方法となっている
大規模事前学習モデル（GPT、BERT、VGGなど）からの転移が一般的
特にデータ量が少ない場合や計算資源が限られている場合に効果的

パラメータ転移は、医療分野や金融分野など、データプライバシーが重要な領域で特に価値があります。また、少量のデータでも高性能なモデルを構築したい場合や、計算リソースが限られている場合に、事前学習済みの大規模モデルからパラメータを転移することで、効率的に目標タスクを解決できます。

2.3節のまとめ

転移方法の比較

事例転移：最も直接的だが、ドメイン間の類似性が高い場合に限られる
特徴転移：異なるデータ構造間での転移が可能
パラメータ転移：現在の主流で、幅広い問題設定に対応可能

選択のポイント

ドメイン間の関係性を正確に把握する
利用可能なデータや計算資源を考慮する
プライバシー要件などの制約を考慮する

次節では、これらの転移方法を具体的に実現するためのアルゴリズムや手法について詳しく見ていきます。

2.4 ドメイン適応問題の分類

ドメイン適応問題の分類

分類の基準

目標ドメインでのラベル付きデータの有無に基づいて分類
主な分類：
- 教師ありドメイン適応（Supervised Domain Adaptation）
- 半教師ありドメイン適応（Semi-supervised Domain Adaptation）
- 教師なしドメイン適応（Unsupervised Domain Adaptation）

各分類の特徴

分類

元ドメイン

目標ドメイン

教師あり

ラベル付きデータあり

半教師あり

ラベル付きデータあり

一部ラベル付きデータあり

教師なし

ラベル付きデータあり

ラベル付きデータなし

ドメイン適応問題の分類は、利用可能なデータの種類と量によって適切な手法を選択する際の重要な指針となります。

2.4.1 教師ありドメイン適応

特徴

目標ドメインでも十分なラベル付きデータが利用可能
元ドメインと目標ドメインの両方で教師あり学習が可能
最も単純なドメイン適応の設定

主なアプローチ

ドメイン間の分布の違いを考慮した重み付け学習
ドメイン不変表現の学習
ドメイン間の特徴量の対応付け

適用例

異なるセンサーからのデータの統合
異なる施設間での医療診断モデルの転移
異なる環境でのロボット制御

教師ありドメイン適応は、目標ドメインでも十分なラベル付きデータが利用できる場合に有効です。ただし、ラベル付きデータの収集コストが高い場合には、他のアプローチを検討する必要があります。

2.4.2 半教師ありドメイン適応

特徴

目標ドメインで限られた量のラベル付きデータのみ利用可能
ラベルなしデータを活用してモデルの性能を向上
実践的な設定として重要

主なアプローチ

自己学習（Self-training）
共学習（Co-training）
グラフベースの半教師あり学習

適用例

医療画像診断（一部の症例のみラベル付き）
自然言語処理（一部の文書のみラベル付き）
異常検知（正常データは豊富、異常データは少ない）

半教師ありドメイン適応は、ラベル付きデータの収集コストが高い実践的な設定で特に有用です。限られたラベル付きデータを効果的に活用する手法が重要となります。

2.4.3 教師なしドメイン適応

特徴

目標ドメインでラベル付きデータが全く利用できない
最も一般的で実践的な設定
最も難しい設定でもある

主なアプローチ

ドメイン不変表現の学習
敵対的学習（Adversarial Learning）
自己教師あり学習（Self-supervised Learning）

適用例

異なるドメイン間での画像認識
異なる言語間での自然言語処理
異なるセンサー間での信号処理

教師なしドメイン適応は、実践的な設定で最も一般的ですが、ラベル付きデータがないため、ドメイン間の関係性を効果的に活用する手法の開発が重要です。

2.4.4 実践的な考慮事項

問題設定の選択

利用可能なデータの種類と量を考慮
計算資源と時間的制約を考慮
期待される性能と実現可能性のバランス

実装上の注意点

データの前処理と正規化
ハイパーパラメータの調整
モデルの評価と検証

実践的なアドバイス

段階的なアプローチの採用
複数の手法の比較検討
継続的なモニタリングと改善

実践的なドメイン適応では、理論的な側面だけでなく、実装上の課題や制約も考慮する必要があります。段階的なアプローチと継続的な改善が成功の鍵となります。

2.4節のまとめ

主要なポイント

ドメイン適応問題は、目標ドメインでのラベル付きデータの有無に基づいて分類される
各分類には適した手法とアプローチが存在する
実践的な設定では、データの制約と計算資源を考慮した選択が重要

今後の展望

より効率的なドメイン適応手法の開発
実践的な課題への対応
新しい問題設定への拡張

ドメイン適応は、転移学習の重要な応用分野として、今後も発展が期待されます。実践的な課題に対応するための新しい手法の開発が求められています。

転移学習（Transfer Learning）

第2章 転移学習の基礎

統合資料

目次

2.1 転移学習の基本問題と目的

本日の内容

転移学習の基本問題

転移学習の基本的な問題意識

3つの基本的な問い

重要な概念

転移学習の目的

転移学習の数学的定義

元ドメインと目標ドメイン

理想的なケース

従来の機械学習と転移学習の違い

従来の機械学習の仮定

転移学習の前提

転移学習を成功させるための3つの基本問題

2.2 いつ転移するか

いつ転移するか（when to transfer）

基本問題

2.2.1 ドメインシフトと転移仮定

ドメインシフトの概念

ドメインシフト（Domain Shift）とは

ドメインシフトの種類

同質的ドメインシフトと異質的ドメインシフト

同質的ドメインシフト（Homogeneous Domain Shift）

同質的ドメインシフトと異質的ドメインシフト（続き）

異質的ドメインシフト（Heterogeneous Domain Shift）

極端なケース：ドメイン一致

転移学習の最も極端なケース

なぜこの場合は単なる機械学習と同等か

近似的ドメイン類似性

現実的なシナリオ

「近さ」の概念

転移仮定の必要性

一般的な状況の課題

同質的ドメインシフトでの転移仮定例

転移仮定の必要性（続き）

異質的ドメインシフトでの転移仮定例

表現学習の役割

転移学習の成功条件

転移学習が成功するための条件

理想的な条件

現実的な条件

同質的・異質的ドメインシフトでの成功条件の違い

転移学習の成功条件（続き）

転移仮定の選択における考慮事項

転移方法の適切な選択

まとめ: ドメインシフトと転移仮定

本節の重要ポイント

2.2.2 確率分布間の距離測度に基づく不一致度

ドメインの不一致度とその重要性

転移学習における前提

不一致度（Discrepancy）の必要性

確率密度比の概念

確率密度比（Density Ratio）の定義

確率密度比の特性

課題

確率密度比の概念（続き）

密度比の推定方法

直接推定アプローチ

密度比推定手法

密度比推定の主要手法

1. カルバック・ライブラー重要度推定法（KLIEP）

密度比推定手法（続き）

2. 制約なし最小二乗重要度適合法（uLSIF）

f-ダイバージェンス

f-ダイバージェンスの定義

f-ダイバージェンスの特性

f-ダイバージェンス（続き）

代表的なf-ダイバージェンス

下界表現による推定

H-ダイバージェンス

H-ダイバージェンスの定義

H-ダイバージェンスの解釈

H-ダイバージェンス（続き）

H-ダイバージェンスの特性

解釈とドメイン識別問題

最大平均不一致度（MMD）

第2章転移学習の基礎