ドメイン適応の理論

本講義では、「ドメイン適応の理論」と題しまして、転移学習の基礎となる教師なしドメイン適応の理論解析について解説します。
前半ではドメイン間距離に基づいた期待リスクの上界について解説し、後半では不可能性定理と呼ばれる期待リスクの下界に関する結果を紹介します。

発表者: [発表者名]
所属: [所属]
日付: [日付]

目次

  1. 期待リスクと経験リスク
  2. 期待リスクの上界評価
  3. 期待リスクの下界評価

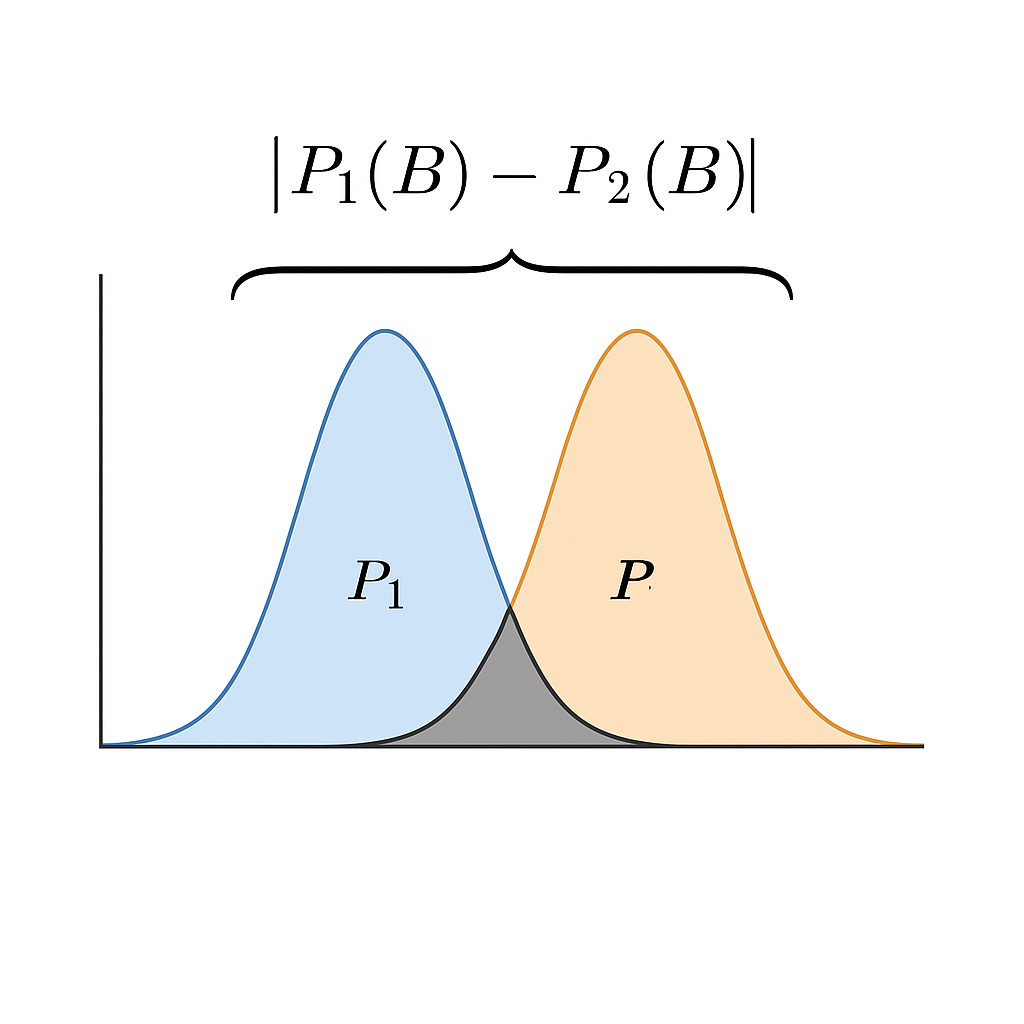
本講義では、転移学習における理論的枠組みとして、ドメイン適応における期待リスクの上界と下界について詳しく解説します。特に重要なのは、VC次元とラデマッハ複雑度の概念です。

期待リスクと経験リスク

転移学習での期待リスクの上界評価を紹介するために、まず単一ドメインで定義される基本的な概念について紹介します。本節の概念について、より詳しくは文献[361]などを参照してください。

画像の代替テキスト 画像の代替テキスト

図1: 期待リスクと経験リスクの概念

期待リスクは、モデルが未知のデータに対してどれだけの誤差を持つかを表す指標です。一方、経験リスクは観測できる訓練サンプル上での誤差です。転移学習の理論では、この二つのリスクの関係を解析することが重要となります。

転移学習では、元ドメインと目標ドメインの間の差異（ドメインシフト）が存在するため、従来の機械学習理論をそのまま適用できないことが問題となります。

定義と記法

入力はさまざまな形式をとりますが、本章では入力は実ベクトルで表されるとします。すなわち入力空間は $\mathcal{X} \subset \mathbb{R}^d$ を満たすと仮定します。また出力空間を集合 $\mathcal{Y}$ で表し、出力空間の元をラベルと呼びます。

基本定義:
- 入力空間: $\mathcal{X} \subset \mathbb{R}^d$
- 出力空間: $\mathcal{Y}$（分類問題では有限集合または連続集合）
- $P$ は直積空間 $\mathcal{X} \times \mathcal{Y}$ 上の同時分布を表す
- 自然数 $m \in \mathbb{N}$ に対し、$(\mathcal{X} \times \mathcal{Y})^m$ 上のサイズ $m$ の独立同一分布を $P^m$ と表す
- 観測値 $D = \{(x_i, y_i)\}_{i=1}^m \sim P^m$ を訓練サンプルと呼ぶ
- テストサンプルも訓練サンプルと独立同一な分布から得られると仮定

出力空間がさまざまな形式をとりえますが、ここでは出力空間が二つの元からなる場合を2値分類、三つ以上の元からなる場合を多値分類と呼びます。

損失関数 $\ell : \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ を考えます。これは、分布 $P$ から得られたサンプル $(x, y)$ に対して、仮説 $h$ の予測がどの程度の誤差を持つかを損失関数 $\ell (y, h(x))$ によって測ります。

転移学習の基礎

転移学習では、入力空間 $\mathcal{X}$ から出力空間 $\mathcal{Y}$ への関数全体からなる集合を $\mathcal{F}(\mathcal{X}, \mathcal{Y})$ と表します。また、$\mathcal{F}(\mathcal{X}, \mathcal{Y})$ の部分集合 $\mathcal{H}=\{h : \mathcal{X} \rightarrow \mathcal{Y}\}$ を仮説集合と呼びます。

仮説に望むことは、訓練サンプルに対して誤差を小さくすることではなく、テストサンプルに対して誤差を小さくすることです。仮説の性能を適切に測るために、ある確率分布 $P$ に対して仮説 $h$ の予測の平均的な誤差は定義1.1における期待リスクとして定義されるのでした。

$R(h, h') = \mathbb{E}_{(x,y) \sim P}[\ell(h(x), h'(x))]$

定義からわかるように、期待リスクは全空間 $\mathcal{X} \times \mathcal{Y}$ 上の期待値になっています。したがって、それは $P$ から得ることができるが、観測していないサンプルに対する誤差についても考慮に入れています。

最適仮説（optimal hypothesis）を、期待リスクを最小化するものと定めます。実際には真の分布 $P$ は未知なので、与えられた仮説に対して期待リスクの計算は不可能であり、最適仮説を直接求めることはできません。

VC次元による上界

仮説空間の複雑度を定量化するための代表的な方法として、ここではVC次元について紹介します。

定義3.1 (VC次元)
2値分類の問題に対し、与えられた仮説集合 $\mathcal{H}$ の VC次元（Vapnik-Chervonenkis dimension）VC($\mathcal{H}$)は、有限部分集合 $\mathcal{X}' \subset \mathcal{X}$ が存在し、$\mathcal{X}'$ 上の任意のラベル付けに対し、ある仮説 $h \in \mathcal{H}$ が存在し、$\mathcal{X}'$ の元のラベルをすべて正しく分類できる場合の、$\mathcal{X}'$ の要素数の最大値を表します。これを数学的に表現すると以下の形になります： $$VC(\mathcal{H}) = \max \left\{ k \in \mathbb{N} \middle| \begin{array}{c} \exists \mathcal{X}' = \{x_1,...,x_k\} \subset \mathcal{X}, \forall y \in \{\pm1\}^k, \\ \exists h \in \mathcal{H}, \forall i \in \{1,...,k\}; h(x_i) = y_i \end{array} \right\}$$

VC次元は有限になるとは限らないことに注意してください。特に、仮説集合を定義するためのパラメータ数は有限であるにも関わらず、その仮説集合のVC次元は無限になる場合があります[241, 1.2.1節]。

定理3.2 (VC次元による上界)
$\mathcal{X}$ を入力空間、$\mathcal{Y} = \{\pm1\}$ を出力空間、$P$ を同時分布とします。$\mathcal{D}$ を $P$ から独立同一に得られたサイズ $m$ のサンプルとし、仮説集合 $\mathcal{H} = \{h : \mathcal{X} \rightarrow \mathcal{Y}\}$ の VC 次元を VC($\mathcal{H}$) とします。$m \geq$ VC($\mathcal{H}$) のとき、任意の $\delta \in (0, 1]$ に対し、少なくとも $1 - \delta$ の確率で以下が成り立ちます： $$\sup_{h \in \mathcal{H}} |\hat{R}_m(h) - R(h)| \leq 2 \sqrt{\frac{VC(\mathcal{H})}{m} \ln \frac{em}{VC(\mathcal{H})}} + \sqrt{\frac{\ln(2/\delta)}{2m}}$$ ここで $e$ はネイピア数を表します。

VC次元による上界の含意

上記の定理の帰結として、任意の仮説 $h \in \mathcal{H}$ と任意の $\delta \in (0, 1]$ に対し、少なくとも $1 - \delta$ の確率で以下が成り立ちます：

$R(h) \leq \hat{R}_m(h) + 2 \sqrt{\frac{VC(\mathcal{H})}{m} \ln \frac{em}{VC(\mathcal{H})}} + \sqrt{\frac{\ln(2/\delta)}{2m}}$

左辺は期待リスクなので、未知の分布に依存しており原理的に計算できません。一方で、仮説集合は既知なので、原理的にはVC次元VC($\mathcal{H}$)も既知と仮定でき、したがって不等式の右辺は計算できます。これより、経験リスクとVC次元から未知の期待リスクの大きさが評価可能であることが明らかになりました。

また定理3.2は、サンプル数が増加するとき、経験リスクの期待リスクへの収束速度がVC次元の小ささに応じて早まることも示しています。

VC次元の有限性は経験リスクが期待リスクへ一様に収束することを保証しています。しかし一方で、実際にはVC次元に基づいた上界はさまざまな不都合を抱えています：
1. 多くの場合は仮説集合に対してそのVC次元を具体的に計算するのは困難
2. VC次元は無限の値をとることがあり、その場合には上界は意味をなさない
3. VC次元はアルゴリズムやサンプルの従う確率分布の情報を考慮に入れていない

ラデマッハ複雑度

次にVC次元のいくつかの問題を解決するために、仮説空間の複雑度の指標としてラデマッハ複雑度と呼ばれる量を導入します。確率1/2で1、確率1/2で−1の値をとる2値確率変数をラデマッハ変数と呼びます。このラデマッハ変数を用いてラデマッハ複雑度は以下のように定義されます。

定義3.3 (ラデマッハ複雑度)
$\mathcal{X}$ 上の確率分布 $P$ から得られたラベルなしサンプル $\mathcal{D} = \{x_i\}_{i=1}^m$ と仮説集合 $\mathcal{H}$ に対し、経験ラデマッハ複雑度 (empirical Rademacher complexity) は以下で定義されます： $$\hat{\mathfrak{R}}_m(\mathcal{H}) = \mathbb{E}_{\kappa=(\kappa_1,...,\kappa_m)} \left[ \sup_{h \in \mathcal{H}} \frac{2}{m} \sum_{i=1}^m \kappa_i h(x_i) \right]$$ ここで $\kappa$ は $m$ 個の独立なラデマッハ変数を表します。仮説集合に対する（期待）ラデマッハ複雑度 (expected Rademacher complexity) は経験ラデマッハ複雑度の期待値として定義されます： $$\mathfrak{R}_m(\mathcal{H}) = \mathbb{E}_{\mathcal{D} \sim P^m} [\hat{\mathfrak{R}}_m(\mathcal{H})]$$

ラデマッハ変数 $\kappa_i$ はサンプル $x_i$ に対する一様ランダムなラベル付けを行った状況と解釈できます。したがって経験ラデマッハ複雑度は、ラベルなしサンプルを固定した場合に、仮説集合がラデマッハ変数で表されるラベル付けにどの程度適応できるかを測っているとみなすことができます。

ラデマッハ複雑度の特徴

ラデマッハ複雑度はVC次元とは異なる状況での複雑度を定義しています。すなわち、ラデマッハ複雑度はラベル付けがランダムな場合に仮説集合の表現能力を測っています。一方で、VC次元はラベル付けが仮説集合にとって最も対応しにくい場合に、仮説集合の表現能力を測っているとみなすことができます。

またラデマッハ複雑度はVC次元とは異なり、ラベルなしサンプルが従う確率分布の情報を用いて定義されています。

以下の定理は経験および期待ラデマッハ複雑度に基づいた期待リスクの上界を与えています[28, 162]。

定理3.4 (ラデマッハ複雑度による上界)
$\mathcal{D} = \{(x_i, y_i)\}_{i=1}^m$ を確率分布 $P$ から独立同一に得られたサイズ $m$ のサンプルとし、$\mathcal{H} \subset \{h : \mathcal{X} \rightarrow \mathcal{Y}\}$ を仮説集合とします。そのとき任意の $\delta \in (0, 1]$ と任意の仮説 $h \in \mathcal{H}$ に対し、少なくとも確率 $1 - \delta$ で以下が成り立ちます： $$R(h) \leq \hat{R}_m(h) + \mathfrak{R}_m(\mathcal{H}) + \sqrt{\frac{\ln \frac{1}{\delta}}{2m}},$$ $$R(h) \leq \hat{R}_m(h) + \hat{\mathfrak{R}}_m(\mathcal{H}) + 3\sqrt{\frac{\ln \frac{2}{\delta}}{2m}}$$

ラデマッハ複雑度とVC次元の関係

特に定理の後半の不等式は経験ラデマッハ複雑度を用いており、VC次元の場合とは異なりサンプル $\mathcal{D}$ に依存した形になっています。ラデマッハ複雑度を用いた上界は、サンプル依存上界（sample-dependent bound）と呼ばれるものの例になっています。

ラデマッハ複雑度はVC次元の定義とは異なった形をしている一方で、その二つは以下の不等式を用いて関連付けることができます[241]：

$$\mathfrak{R}_m(\mathcal{H}) \leq 2\sqrt{\frac{4}{m} \left(VC(\mathcal{H}) \ln \frac{2em}{VC(\mathcal{H})} + \ln \frac{4}{\delta} \right)}$$

この結果はラデマッハ複雑度を用いた上界とVC次元を用いた上界を密接に結びつけています。

ターゲットとソースドメインの期待リスク(準備)

定義3.5（全変動距離）

$\mathcal{B}$ を可測集合全体とし、$P_1$ と $P_2$ を確率分布とします。このとき $P_1$ と $P_2$ の間の全変動距離（total variation distance）または $L^1$ 距離を以下で定めます。

$D_{\text{TV}}(P_1, P_2) = 2 \sup_{B \in \mathcal{B}} |P_1(B) - P_2(B)|$

全変動距離は、二つの確率分布が同一の事象 $B$ に与える確率の差の最大値で、確率分布空間上の距離になることが知られています。

全変動距離は、二つの確率分布がどれだけ異なっているかを直接的に測る尺度です。転移学習では、元ドメインと目標ドメインの分布の違いを定量化するために用いられます。

概念図: 全変動距離を視覚化したもの
$|P_1(B) - P_2(B)| $でsupをとるには $\{P_1 < P_2\}$ または $\{P_1 > P_2\}$で大きい方をとる

図1: 全変動距離の概念

全変動距離による上界（定理3.6）

定理3.6（全変動距離による上界）

ラベル空間を $\mathcal{Y} = \{0, 1\}$ とし、損失関数を 0-1 損失 $\ell_{01}$ とします。空間 $\mathcal{X} \times \mathcal{Y}$ 上の二つの確率分布 $P^S$, $P^T$ と、仮説集合 $\mathcal{H}$ が与えられたとき、任意の $h \in \mathcal{H}$ に対し以下が成り立ちます。

$R_T(h) \leq R_S(h) + D_{\text{TV}}(P^S_X, P^T_X) + \min\{E_{P^S_X}[|f_S(X) - f_T(X)|], E_{P^T_X}[|f_S(X) - f_T(X)|]\}$

ここで $P^S_X$ と $P^T_X$ はそれぞれ $P^S$ と $P^T$ の $\mathcal{X}$ 上の周辺分布、$f_S$ と $f_T$ はそれぞれ $P^S$ と $P^T$ に関する元ドメインと目標ドメインのラベル付け関数です。

上記の定理では、仮説 $h$ の目標ドメインでの期待リスクを、元ドメインの期待リスクを用いて上から評価しています。しかし全変動距離で表されるドメイン間距離には以下のような制限があります：

これらの問題に対処するために、ベンデイビッドらは仮説集合に関するドメイン間のダイバージェンスを定義しました。

対称差H-ダイバージェンス

全変動距離の問題に対処するために、ベンデイビッドらは仮説集合に関するドメイン間のダイバージェンスを定義しました。このダイバージェンスについて説明するために、いくつかの記号を導入します。

二つの仮説 $g, g' : \mathcal{X} \rightarrow \mathcal{Y} = \{0, 1\}$ に対し、対称差仮説を $x \mapsto g(x) \oplus g'(x)$ で定義します。ここで $\oplus$ は排他的論理和を表します。また仮説集合 $\mathcal{H}$ に対し、対称差仮説集合を以下で定義します。

$\mathcal{H} \Delta \mathcal{H} := \{g \oplus g' | g, g' \in \mathcal{H}\}$

また以下では $I_h \subset \mathcal{X}$ を $h \in \mathcal{H} \Delta \mathcal{H}$ の合集合とします。すなわち $x \in I_h \Leftrightarrow h(x) = 1$ と定めます。このとき仮説集合 $\mathcal{H} \Delta \mathcal{H}$ に対して定めた $\mathcal{H}$-ダイバージェンス $D_{\mathcal{H} \Delta \mathcal{H}}(P^S_X, P^T_X)$ を対称差 $\mathcal{H}$-ダイバージェンスと呼ぶことにします。

対称差 $\mathcal{H}$-ダイバージェンスは、定義から仮説集合 $\mathcal{H}$ を考慮に入れていることがわかります。また対称差 $\mathcal{H}$-ダイバージェンスは常に全変動距離よりも大きくはならないことが知られており、したがってそれは全変動距離を用いるよりも精緻（tight）な上界を導くことにつながります。

定理3.7：対称差H-ダイバージェンスによる上界

定理 3.7（対称差H-ダイバージェンスによる上界）:
$\mathcal{H}$ を仮説集合とし、損失関数を 0-1 損失 $\ell_{01}$ とします。任意の $h \in \mathcal{H}$ に対し以下が成り立ちます：
$R_T(h) \leq R_S(h) + \frac{1}{2}D_{\mathcal{H}\Delta\mathcal{H}}(P^S_X, P^T_X) + \lambda$
ここで $\lambda$ は以下で定義される最小同時誤差を表します：
$\lambda := \min_{h\in\mathcal{H}} R_S(h) + R_T(h)$

この定理は、転移学習における期待リスクの上界を与える基本的な結果です。上界は3つの項から構成されています：

  1. ソースドメインでのリスク $R_S(h)$：通常、訓練データから計算可能
  2. ドメイン間の差異 $D_{\mathcal{H}\Delta\mathcal{H}}(P^S_X, P^T_X)$：対称差H-ダイバージェンスとして知られる指標で、二つのドメインの周辺分布がどれだけ異なるかを測ります
  3. 最小同時誤差 $\lambda$：理論的に達成可能な最小リスクを表し、ラベル分布の違いに関連します

この定理は「領域適応のセオリー」と呼ばれることもあり、特にドメイン適応型転移学習において中心的な役割を果たします。実用上の課題は、対称差H-ダイバージェンスの計算が一般的に困難であることです。

定義3.8：不一致度（Discrepancy Distance）

定義 3.8（不一致度）:
$\mathcal{X} \times \mathcal{Y}$ 上の二つの確率分布 $P^S$ と $P^T$ が与えられたとします。また $\mathcal{H}$ を仮説集合、$\ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ を損失関数とします。このとき $\mathcal{X}$ 上の周辺分布 $P^S_X$ と $P^T_X$ の間の不一致度（discrepancy distance）は以下で定義されます：
$D_\ell(P^S_X, P^T_X) = \sup_{(h,h')\in\mathcal{H}^2} \left| \mathbb{E}_{x\sim P^S_X}[\ell(h'(x), h(x))] - \mathbb{E}_{x\sim P^T_X}[\ell(h'(x), h(x))] \right|$

不一致度は、二つのドメイン間の差異を測る指標で、以下の特徴があります：

不一致度は特に回帰問題や、0-1損失以外の損失関数を使用する問題において重要です。また、この定義により、ドメイン適応の理論をより幅広い学習問題に拡張することができます。

命題3.9：不一致度と全変動距離の関係

命題 3.9:
$\mathcal{X} \times \mathcal{Y}$ 上の二つの確率分布 $P^S$ と $P^T$ が与えられたとします。$\mathcal{H}$ を仮説集合、$\ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ を $M$-有界な非負の損失関数とします。このとき任意の仮説集合 $\mathcal{H}$ に対し、以下が成り立ちます：
$D_\ell(P^S_X, P^T_X) \leq M \cdot D_{TV}(P^S_X, P^T_X)$

この命題は、不一致度と全変動距離（Total Variation Distance）の間の関係を示しています。重要なポイントは：

全変動距離は確率論で最も基本的な距離指標の一つですが、高次元空間では推定が困難です。この命題は、不一致度が全変動距離に関連しつつも、計算上の利点を持つ可能性を示唆しています。

命題3.10：経験不一致度の上界

命題 3.10:
$\mathcal{H}$ を仮説集合、$\ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ を $M$-有界な損失関数とします。また $\mathcal{H}$ から定まる関数の集合を
$L_\mathcal{H} = \{(\mathcal{X} \rightarrow \ell(h'(x), h(x)) | h, h' \in \mathcal{H}\}$
と定めます。$P_X$ を $\mathcal{X}$ 上の分布とし、$\hat{P}_X$ をサンプル $\mathcal{D} = (x_1, \ldots, x_m)$ に対応する経験分布とします。このとき任意の $\delta \in (0, 1)$ に対し、少なくとも $1 - \delta$ の確率で以下が成り立ちます：
$D_\ell(P_X, \hat{P}_X) \leq \hat{\mathfrak{R}}_m(L_\mathcal{H}) + 3M\sqrt{\frac{\log \frac{2}{\delta}}{2m}}$

この命題は、真の分布と経験分布の間の不一致度の上界を与えています：

この結果は、有限サンプルから不一致度を推定する際の統計的保証を与えています。これにより、実際の適用場面で経験分布から計算された不一致度がどの程度信頼できるかを評価できます。

命題3.11：サンプルに基づく不一致度の上界

命題 3.11:
$P^S$ と $P^T$ を $\mathcal{X} \times \mathcal{Y}$ 上の確率分布とします。$\mathcal{H}$ を仮説集合とし、損失関数 $\ell_q: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ は $\ell_q(y, y') = |y - y'|^q$ で定義され、$\mathcal{Y}$ 上で $M$-有界とします。また $\hat{P}^S_X$ と $\hat{P}^T_X$ を $P^S_X$ と $P^T_X$ から独立に得られたサイズ $m_S$ と $m_T$ のサンプルから定まる経験分布とします。このとき任意の $\delta \in (0, 1)$ に対し、少なくとも $1 - \delta$ の確率で以下が成り立ちます：
$D_{\ell_q}(P^S_X, P^T_X) \leq D_{\ell_q}(\hat{P}^S_X, \hat{P}^T_X) + 4q(\hat{\mathfrak{R}}^S_{m_S}(\mathcal{H}) + \hat{\mathfrak{R}}^T_{m_T}(\mathcal{H})) + 3M\left(\sqrt{\frac{\log(\frac{4}{\delta})}{2m_S}} + \sqrt{\frac{\log(\frac{4}{\delta})}{2m_T}}\right)$

この命題は、よく使われる $q$乗損失関数に対して、真の不一致度と経験不一致度の関係を明らかにしています：

この命題は、回帰問題などでよく使われる $q$乗損失関数（例えば $q=2$ で2乗誤差）に対する不一致度の推定方法を示しています。実践的な転移学習では、この上界を用いて経験的に計算した不一致度がどの程度信頼できるかを評価できます。

定理3.12：不一致度による上界

定理 3.12（不一致度による上界）:
$P^S$ と $P^T$ を $\mathcal{X} \times \mathcal{Y}$ 上の確率分布とします。$\mathcal{H}$ を仮説集合、$\ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{\geq 0}$ を対称で三角不等式を満たし、かつ有界な損失関数とします。そのときそれぞれの確率分布に対する最適仮説
$h^*_S = \arg\min_{h \in \mathcal{H}} R_S(h), \quad h^*_T = \arg\min_{h \in \mathcal{H}} R_T(h)$
は任意の $h \in \mathcal{H}$ に対し以下を満たします：
$R_T(h) \leq R_S(h, h^*_S) + D_\ell(P^S_X, P^T_X) + \varepsilon$
ここで、$\varepsilon = R_T(h^*_T) + R_S(h^*_T, h^*_S)$ とおきました。

この定理は、定理3.7（対称差H-ダイバージェンス）と似た構造を持ち、ターゲットドメインでのリスクを上界評価します：

文献[197]によれば、いくつかの状況では定理3.12の上界は定理3.7の上界より精緻（tight）になることが示されています。特に仮説 $h \in \mathcal{H}$ が一つしかない場合や、$h^* = h^*_S = h^*_T$ である場合に、定理3.12の上界は定理3.7の上界よりも小さくなります。

補題3.13：分布の同一性の必要十分条件

補題 3.13（分布の同一性の必要十分条件）:
分布 $P^S_X$ と $P^T_X$ が同一であるための必要十分条件は、任意の連続微分可能な関数 $f$ に対し以下が成り立つことです：
$\mathbb{E}_{x \sim P^S_X}[f(x)] = \mathbb{E}_{x \sim P^T_X}[f(x)]$

この補題は、確率分布の同一性を判定するための基準を提供しています：

この補題から、二つの分布が異なる場合、必ず期待値が異なる関数が存在することがわかります。さらに、異なる分布間の「距離」を測るために、関数クラスに対する期待値の差の最大値（上限）を考えるというアイデアが生まれます。これが積分確率計量（IPM）につながる重要な洞察です。

積分確率計量（IPM）

対称差H-ダイバージェンスや不一致度は計算が困難という問題を持っています。そこで、計算がより容易で、かつ理論的に有用な距離指標として積分確率計量（Integral Probability Metric, IPM）が導入されました。

定義 3.14（積分確率計量）:
可測空間 $\mathcal{X}$ 上の分布 $P^S_X$ と $P^T_X$ に対し、関数族 $\mathcal{F}$ に関する積分確率計量（IPM）は以下で定義されます：
$D_{\mathcal{F}}(P^S_X, P^T_X) = \sup_{f \in \mathcal{F}} \left| \mathbb{E}_{x \sim P^S_X}[f(x)] - \mathbb{E}_{x \sim P^T_X}[f(x)] \right|$

IPMは二つの確率分布がどの程度異なるかの指標を与えており、それらは機械学習において多くの応用を持ちます。一般に、任意の関数クラス $\mathcal{F}$ に対し、$D_{\mathcal{F}}(P, Q)$ は擬距離にはなりますが、距離の公理を満たすとは限りません。

IPMはドメイン間の違いを定量化する柔軟な方法です。適切な関数クラス $\mathcal{F}$ を選ぶことで、様々な性質を持つ距離指標を定義できます。特に、次のスライドで紹介するワッサースタイン距離や最大平均不一致度（MMD）は、IPMの特別な場合として解釈できます。

ワッサースタイン距離と上界

ワッサースタイン距離は、IPMの一種として定義される距離指標で、特に構造のある空間上の確率分布に対して有用です。

定理 3.15（ワッサースタイン距離による期待リスクの上界）:
$(\mathcal{X}, d)$ を距離空間、$P^S$ と $P^T$ を $\mathcal{X} \times \mathcal{Y}$ 上の確率分布、$\ell(y, y') := |y - y'|$ を損失関数とします。$\mathcal{H}$ を仮説集合とし、任意の仮説 $h \in \mathcal{H}$ は $K$-リプシッツ関数であるとします。このとき、以下が成り立ちます：
$R_T(h) \leq R_S(h) + 2K D_W(P^S_X, P^T_X) + \lambda$
ここで $\lambda$ は以下で定められます：
$\lambda = \min_{h \in \mathcal{H}} R_S(h) + R_T(h)$
証明（概略）:
任意の仮説 $h$ と $h'$ は $K$-リプシッツなので、$|h-h'|$ は $2K$-リプシッツ関数になります。したがって
$R_T(h, h') - R_S(h, h') \leq \sup_{f: 2K-リプシッツ} \mathbb{E}_{P^T_X}[f] - \mathbb{E}_{P^S_X}[f] = 2K D_W(P^S_X, P^T_X)$
これより様々な不等式の操作を経て目的の上界が導出されます。詳細は省略します。

定理3.15では真の周辺分布 $P^S_X$, $P^T_X$ を用いた期待リスクの上界評価が与えられています。しかし、実際には真の周辺分布は未知であり、経験分布のみが観測されます。そのため、実用的な上界評価には、経験分布からワッサースタイン距離を推定する手法が必要となります。

最大平均不一致度（MMD）

本節ではカーネル法に基づいたIPMである最大平均不一致度（Maximum Mean Discrepancy, MMD）について取り上げます。

カーネル法の基本:
カーネル法は、データ解析を行う際にデータの非線形性や高次モーメントを取り込むための方法の一つです。データ空間 $\mathcal{X}$ に対し、対称性と正定値性を満たす関数 $k: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$ をカーネル（kernel）関数と呼びます。代表的な正定値カーネルとして線形カーネル、多項式カーネル、ガウスカーネルなどがあります。
定義 3.18（カーネル平均）:
$k: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$ をカーネルとし、その再生核ヒルベルト空間を $\mathcal{H}$、特徴写像を $\phi(x) = k(\cdot, x)$ とします。$\mathcal{X}$ 上の確率分布 $P_X$ が与えられたとき、写像
$\mu[P_X] := \mathbb{E}_{x \sim P_X}[\phi(x)]$
をカーネル平均（kernel mean）と呼びます。
命題 3.19（最大平均不一致度のカーネル平均による表現）:
カーネルは $\mathbb{E}_{x \sim P_X}[k(x, x)] < \infty$ を満たすとします。
$\mathcal{F} = \{f \in \mathcal{H}_k : \|f\|_{\mathcal{H}_k} \leq 1\}$
とおくとき、以下が成り立ちます：
$D_{\text{MMD}}(P^S_X, P^T_X) = \|\mu[P^S_X] - \mu[P^T_X]\|_{\mathcal{H}_k}$
ここで $\|\cdot\|_{\mathcal{H}_k}$ は $k$ の再生核ヒルベルト空間のノルムを表しています。

MMDは有限のサンプルから近似計算ができるので、対称差H-ダイバージェンスや不一致度などに対して計算量の点で優位性を持ちます。

期待リスクの下界と不可能性定理

ここまでは期待リスクの上界に関する評価について紹介してきました。一方で、本節では不可能性定理（impossibility theorem）と呼ばれる期待リスクの下界に関する評価について紹介します。

不可能性定理の概念:
不可能性定理とは、どんなアルゴリズムを用いても超えることのできない理論限界を表すものです。転移学習の文脈では、ソースドメインとターゲットドメインの分布の違いがある場合に、どれだけ精度よくターゲットドメインでの性能を予測できるかの限界を示します。

単一ドメインにおける不可能性定理として有名なノーフリーランチ定理（no-free-lunch theorem）は、特定の仮定なしにはあらゆるアルゴリズムが平均的に同じ性能しか出せないことを示しています。

転移学習の設定では、ドメイン間の分布の違いがある場合、ソースドメインでの性能がいかに良くても、その知識をターゲットドメインに転用する際には理論的な限界が存在することが示されています。

この不可能性定理は、単にネガティブな結果というわけではなく、転移学習を効果的に行うためには、ドメイン間の関係に関する何らかの仮定や知識が必要であることを示唆しています。そのため、実践的な転移学習手法では、ドメイン間の関係を考慮した手法設計が重要となります。

期待リスクの下界評価

本節では不可能性定理（impossibility theorem）と呼ばれる期待リスクの下界に関する評価について紹介します。これらの結果はどんなアルゴリズムを用いても超えることのできない理論限界を表すものです。

3.1節までは、期待リスクの上界に関する評価について紹介してきました。一方で、本節では不可能性定理と呼ばれる期待リスクの下界に関する評価について紹介します。

不可能性定理を扱う前に、単一ドメインにおける不可能性定理として有名なノーフリーランチ定理（no-free-lunch theorem）について紹介します。

期待リスクの下界の意味

期待リスクの下界評価は、最良のアルゴリズムを用いても理論的には避けられない最小限のエラーを示します。

この下界は、アルゴリズム設計の限界を理解するために重要な指標となります。

不可能性定理の概要

不可能性定理は、特定の条件下では転移学習が原理的に不可能であることを示すものです。特に、ドメイン間の関係に関する事前知識がない場合、転移学習の成功は保証できません。

不可能性定理の主な主張

1. 単一ドメインの場合: ノーフリーランチ定理により、事前知識なしで学習が困難になる

2. 転移学習の場合: 元ドメインと目標ドメインの関係性に関する知識がなければ、元ドメインのみで学習を行った仮説は目標ドメインで高い性能を発揮することは期待できない

次に、単一ドメインでの学習と転移学習における不可能性定理の詳細を見ていきます。特に、文献において指摘された基本的な事実を紹介します。すなわち、最小同時誤差 $\lambda$ が大きい場合は、元ドメインと目標ドメインの両方で有効に働く仮説は存在せず、したがって元ドメインのみで学習を行った仮説は目標ドメインで高い性能を発揮することは期待できないというものです。

学習アルゴリズムの定義

定義 3.20 （学習アルゴリズム）

仮説空間 $\mathcal{H}$ に関する学習アルゴリズム（learning algorithm）とは以下の関数を指します。

$\mathcal{A}: \bigcup_{m=1}^{\infty} (\mathcal{X} \times \mathcal{Y})^m \rightarrow \mathcal{H}$

すなわち学習アルゴリズムとは、$m$ 個のラベルありデータを入力すると、仮説を出力する関数のことです。これは関数を出力する関数であることに注意してください。

サンプルはある確率分布から独立同一に得られるとします。独立同一性は、サンプル内の各データは真の確率分布に関する何らかの新しい情報を持っていることを表します。このときサンプルサイズが無限に増加していけば、適切に設計されたアルゴリズムの出力は最適仮説に近付いていくことが期待できます。

しかしノーフリーランチ定理によると、サンプル以外にタスクに関する事前知識がなければ、どんな学習アルゴリズムに対しても苦手とするタスクが存在することが明らかになります。

ノーフリーランチ定理

定理 3.21 （ノーフリーランチ定理）

$\mathcal{X}$ を入力空間、$\mathcal{Y} = \{±1\}$ をラベル空間とし、自然数 $m$ は $m \leq |\mathcal{X}|/2$ を満たすとします。また損失関数は 0-1 損失 $\ell$ であるとします。仮説空間が $\mathcal{X}$ から $\mathcal{Y}$ へのすべての関数の集合であるとき、任意の学習アルゴリズム $\mathcal{A}$ に対し、$\mathcal{X} \times \mathcal{Y}$ 上の確率分布 $P$ が存在し、以下が成り立ちます。

(I) 関数 $f: \mathcal{X} \rightarrow \mathcal{Y}$ が存在し $R_P(f) = 0$.

(II) $R_{\mathcal{D} \sim P^m}(\mathcal{A}(\mathcal{D})) \geq \frac{1}{4}$.

この定理は、入力空間$\mathcal{X}$が無限集合であるような状況を考えると理解しやすくなります。そのような状況ではサンプルサイズは常に $m \leq |\mathcal{X}|/2$ を満たすことになります。

ノーフリーランチ定理によれば、タスクの事前情報がない場合、どれだけサンプルサイズを増やしても、アルゴリズムが任意のタスクに対して最適な予測器を精度よく近似することはできません。言い換えると、タスクに関してまったく未知の状態で、すべてのタスク上で一様にうまくいくようなアルゴリズムは存在しないことを示しています。

転移学習アルゴリズムの定義

定義 3.22 （転移学習アルゴリズム）

仮説空間 $\mathcal{H}$ に関する転移学習アルゴリズムとは以下の関数を指します。

$\mathcal{A}: \bigcup_{m=1}^{\infty} \bigcup_{n=1}^{\infty} (\mathcal{X} \times \mathcal{Y})^m \times \mathcal{X}^n \rightarrow \mathcal{H}$

すなわち転移学習アルゴリズムとは、$m$ 個の元ドメインのラベルありデータと $n$ 個の目標ドメインのラベルなしデータを入力すると、目標ドメインでの仮説を出力する関数のことです。

ここでは同質的な状況（すなわち元ドメインと目標ドメインで$\mathcal{X}$が同一の状況）を仮定していますが、定義域の空間を変更することで異質的な状況へ定義を拡張することが可能です。

転移学習においては、元ドメインと目標ドメインの関係に関する事前知識がなければ、転移学習の成功を保証することはできません。次に、この事実について説明します。

学習可能性

定義 3.23 （学習可能性）

$\mathcal{H}$ を仮説集合、$\mathcal{A}$ を転移学習アルゴリズムとします。また、$\varepsilon > 0, 0 < \delta < 1$ とし $m, n$ を正の整数とします。さらに $\mathcal{D}_S$ を分布 $P^S$ によって独立同一に生成されたサイズ $m$ のラベル付きサンプル、$\mathcal{D}_{T,X}$ を分布 $P^T_X$ によって独立同一に生成されたサイズ $n$ のラベルなしサンプルとします。以下を満たすとき、$\mathcal{A}$ は $\mathcal{H}$ に関して $P^S$ から $P^T_X$ を $(\varepsilon, \delta, m, n)$-学習可能といいます。

$\mathrm{Pr} [R_T (\mathcal{A}(\mathcal{D}_S, \mathcal{D}_{T,X})) \leq R_T(\mathcal{H}) + \varepsilon] \geq 1 - \delta$

ここで左辺では、$\mathcal{D}_S$ と $\mathcal{D}_{T,X}$ に関する確率を $\mathrm{Pr}$ で表しています。

すなわちアルゴリズムが $(\varepsilon, \delta, m, n)$-学習可能な状況というのは、元ドメインと目標ドメインにそれぞれ $m$ 個と $n$ 個のデータがあれば、高い確率で最適仮説に近い性能の仮説を出力できるということを表しています。

注意として、アルゴリズムの出力 $\mathcal{A}(\mathcal{D}_S, \mathcal{D}_{T,X})$ の性能が最適仮説 $h^*$ の性能に近いからといって、必ずしも $\mathcal{A}(\mathcal{D}_S, \mathcal{D}_{T,X})$ と $h^*$ が仮説空間の何らかの距離で近いことを保証するものではありません。

この学習可能性の定義は、与えられたアルゴリズムが理論的な性能保証を持つかどうかを判定するための基準を与えています。この学習可能性の意味では、定義中の $\varepsilon$ と $\delta$ を小さくできるほどよいアルゴリズムということができます。

転移学習の不可能性定理（仮定A2の必要性）

定理 3.24 （仮定(A2)の必要性）

$\mathcal{X} = \{0, 1\}$ を入力空間、$\mathcal{Y} = \{0, 1\}$ をラベル空間とします。また仮説空間 $\mathcal{H}$ は $\mathcal{X}$ から $\mathcal{Y}$ への関数全体とします。そのとき $\mathcal{X} \times \mathcal{Y}$ 上の分布 $P^S$ と $\mathcal{X}$ 上の分布 $P^T$ が存在し、任意の転移学習アルゴリズムと任意の正整数 $m, n$ に対し、あるラベル付け関数 $f: \mathcal{X} \rightarrow \mathcal{Y}$ が存在し以下を満たします。

1. 仮定 (A1) を満たす。

2. 仮定 (A3) を満たす。

3. $1/2$ 以上の確率で $R_f (\mathcal{A}(\mathcal{D}_S, \mathcal{D}_{T,X})) \geq \frac{1}{2}$ が成り立つ。

ここで $R_f$ は $P^T_{Y|X} = f$ という決定的な分布に対する期待リスクを表します。

この結果は、仮定(A2)で表されるドメイン間の周辺分布の差が小さいという条件の重要性を示しています。

仮定(A1)の共変量シフトは、ラベル付けする確率分布がドメイン間で共通になっているという条件で、理論的に詳細な研究が行われています。一方、仮定(A2)は周辺分布の類似性に関する条件で、転移学習に関するよい期待リスクの上界を得るために、多くの既存研究が採用しているものです。

転移学習の不可能性定理（仮定A3の必要性）

定理 3.25 （仮定(A3)の必要性）

$\mathcal{X} = [0, 1]$ を入力空間、$\mathcal{Y} = \{0, 1\}$ をラベル空間とします。また $0 < t < 1$ に対し $h_t$ を $\mathcal{X}$ 上の階段関数

$h_t(x) = \begin{cases} 0 & 0 \leq x \leq t \\ 1 & t < x \leq 1 \end{cases}$

とし、仮説空間を $\mathcal{H} = \{h_t | 0 < t < 1\}$ とします。そのとき任意の $0 < \varepsilon < 1$ に対し $\mathcal{X} \times \mathcal{Y}$ 上の分布 $P^S$ と $\mathcal{X}$ 上の分布 $P^T_X$ が存在し、任意の転移学習アルゴリズムと任意の正整数 $m, n$ に対し、あるラベル付け関数 $f: \mathcal{X} \rightarrow \mathcal{Y}$ が存在し以下を満たします。

1. 仮定 (A1) を満たす。

2. 仮定 (A2) を満たす。

3. $1/2$ 以上の確率で $R_f (\mathcal{A}(\mathcal{D}_S, \mathcal{D}_{T,X})) \geq \frac{1}{2}$ が成り立つ。

この結果は、仮定(A3)で表される同時誤差が小さいという条件の重要性を示しています。

定理3.24と定理3.25からの帰結として、仮定(A1)を満たしたとしても、仮定(A2)と仮定(A3)のいずれかを満たさない場合は教師なし転移学習をするのに十分ではありません。言い換えると転移学習問題の解決はそれら二つの条件を必要とします。