第9章メタ学習

統合版

転移学習（機械学習プロフェッショナルシリーズ）

勉強会資料

作成日：2025年8月

第9章目次

9.1 機械学習における機能バイアスとその学習
- 9.1.1 概念学習とバージョン空間
- 9.1.2 機能バイアスとその学習
9.2 統計的メタ学習の定式化
- 9.2.1 統計的メタ学習への導入
- 9.2.2 統計的メタ学習の定式化
  - 9.2.2.1 メタ期待リスクとメタ経験リスク
  - 9.2.2.2 メタ経験リスクによる近似の精度評価
  - 9.2.2.3 メタ訓練とメタテスト
- 9.2.3 より一般的なメタ学習の定式化
- 9.2.4 メタ知識の学習
  - 9.2.4.1 2レベル最適化による学習の定式化
  - 9.2.4.2 線形回帰タスクの環境におけるメタ知識の学習の例
9.3 メタ学習の分類と方法
- 9.3.1 メタ学習の分類の概要
- 9.3.2 メタ知識の表現に基づく分類と方法
  - 9.3.2.1 モデルパラメータの初期値としてのメタ知識の学習
  - 9.3.2.2 オプティマイザとしてのメタ知識の学習
  - 9.3.2.3 Sim2Real転移のためのメタ学習
9.4 まとめ

第9章の概要

本章で扱う内容

メタ学習の基本概念：帰納バイアス学習としてのメタ学習
統計的メタ学習の定式化：複数タスクに共通する最適な仮説集合
メタ学習の分類：メタ目的、メタオプティマイザ、メタ表現の観点による分類
メタ知識の表現：モデルパラメタやオプティマイザの表現
Sim2Real：シミュレーションから実世界への転移

9.1 機械学習における帰納バイアスとその学習

メタ学習とは

メタ学習

複数のタスクからそれらに共通する知識を学習する手法

メタ学習の特徴

帰納バイアス学習や学習のための学習とも呼ばれる
転移学習に関連するトピックの中でも歴史のある分野
アルゴリズムに「どのようなモデルを出力させるか」を決定する指針を学習

本章では、複数のタスクから共通する知識を学習するメタ学習について説明します。メタ学習は転移学習の一種として位置づけられる重要な手法です。

9.1.1 概念学習とバージョン空間

概念学習の基本例

ウォータースポーツの楽しみ方を予測

問題設定：「友人が大好きなウォータースポーツを楽しむ日」を予測したい

特徴量（6つの属性）

$x_1$：天気
$x_2$：気温
$x_3$：湿度
$x_4$：風
$x_5$：水温
$x_6$：天気予報

これらの特徴量 $\mathbf{x} = (x_1, x_2, x_3, x_4, x_5, x_6)$ からウォータースポーツを楽しんだこと（$y = 1$）を推定する

仮説の数学的表現

仮説 $h(\mathbf{x})$：

$$h(\mathbf{x}) = \langle x_1, x_2, \ldots, x_6 \rangle$$ $$= \begin{cases} 1 & \text{if } (x_1 = *) \land (x_2 = *) \land \cdots \land (x_6 = *) \\ 0 & \text{otherwise} \end{cases}$$

記号の意味

$\land$：論理積を表す記号
$*$：各特徴の何らかの値が入ることを表す
例：$h_1(\mathbf{x}) = \langle$晴れ, *, *, 強い, *, *$\rangle$ → 「風の強い晴れの日」
例：$h_2(\mathbf{x}) = \langle$晴れ, *, *, *, *, *$\rangle$ → 「晴れの日」

このような形式の仮説を表9.1のような与えられたデータから決定するのがこの問題における学習です。これは概念学習（concept learning）と呼ばれます。

概念学習における訓練データの例

表9.1の内容：概念学習における訓練データの例

データID	天気	気温	湿度	風	水温	天気予報	楽しんだ
1	晴れ	暖かい	普通	強い	温かい	当たり	はい
2	晴れ	暖かい	高い	強い	温かい	当たり	はい
3	雨	寒い	高い	強い	温かい	はずれ	いいえ
4	晴れ	暖かい	高い	強い	冷たい	はずれ	はい

特徴の値域

天気：{晴れ, 曇り, 雨}
気温：{暖かい, 寒い}
湿度：{高い, 普通}
風：{強い, 弱い}
水温：{温かい, 冷たい}
天気予報：{当たり, はずれ}

バージョン空間（Version Space）

バージョン空間：有限の訓練データに基づいて仮説を学習するとき、訓練データを完全に説明する複数の仮説が存在し得る。そのような仮説の集合

表9.1のデータに対するバージョン空間の例

$h_1(\mathbf{x}) = \langle$晴れ, 暖かい, *, 強い, *, *$\rangle$

$h_2(\mathbf{x}) = \langle$晴れ, *, *, 強い, *, *$\rangle$

$h_3(\mathbf{x}) = \langle$晴れ, 暖かい, *, *, *, *$\rangle$

仮説集合のサイズ

各特徴には「任意の値をとってもよい」選択肢がある
「どんな特徴xにおいてもウォータースポーツを楽しむ日にはならない」仮説$h_0$も必要
意味的に異なる仮説の個数：$4 \times 3^5 + 1 = 973$

9.1.2 帰納バイアスとその学習

バージョン空間における問題

学習アルゴリズムの課題

バージョン空間の元である仮説は、学習に用いた訓練データに対してはすべて同じ性能を示す
しかし、未知の事例に対しては異なる予測を返す可能性がある

具体例

事例： $\mathbf{x} = ($晴れ, 寒い, 普通, 強い, 温かい, 当たり$)$

$h_2$ を仮説とすると：$y = 1$
$h_3$ を仮説とすると：$y = 0$

学習アルゴリズムは訓練データの観点からは同じ性能を持つ仮説の中から、より良い予測をする仮説を選ぶ必要があります。

オッカムの剃刀（Occam's Razor）

オッカムの剃刀

データをうまく説明する複数の仮説がある場合、その中で最もシンプルな仮説を用いるべきである

回帰問題への適用例

図9.1：シンプルな仮説と複雑な仮説の例

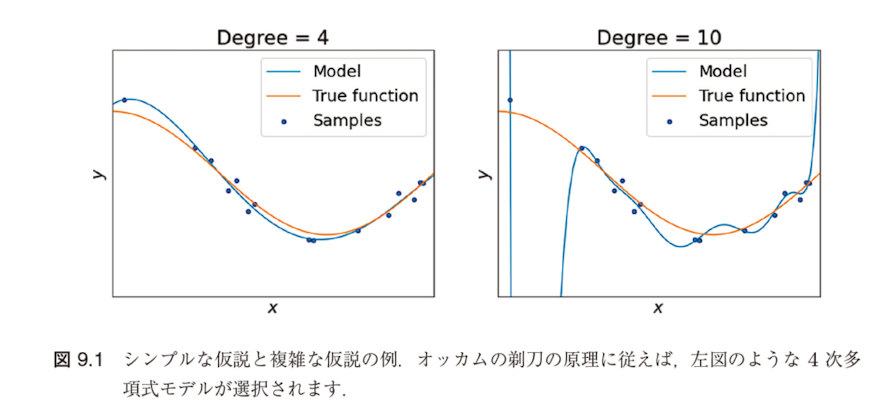
4次多項式モデル vs 10次多項式モデル

両者とも訓練データに対して同程度の性能を示すが、オッカムの剃刀の原理に従えば4次多項式モデルが選択される

オッカムの剃刀は絶対的な原理ではありません。同等の訓練誤差を達成したうえで、10次多項式の方が4次多項式より汎化するモデルとなるような問題も現実には考えられます。

帰納バイアスとは

帰納バイアス：「どのような仮説がよりよいか」という、仮説（予測モデル）に対する一段階メタな仮説を表すもの

帰納バイアスの重要性

あるタスクにおいて、学習アルゴリズムの持つ帰納バイアスがそのタスク自体にマッチするかどうかが学習される仮説の性能を決定する要因
与えられたタスクおよびそのタスクにおけるデータから帰納バイアスそのものを学習したい

メタ学習の動機

これが帰納バイアス学習（inductive bias learning）またはメタ学習（meta-learning）の動機付けになります

9.2 統計的メタ学習の定式化

9.2.1 統計的メタ学習への導入

メタ学習の目的と課題

メタ学習の目的

帰納バイアスを学習すること

従来のアプローチの限界

帰納バイアス = 仮説の選び方に関する指針
学習アルゴリズムに帰納バイアスを持たせるには、最適な仮説を一つだけ含む仮説集合 $\mathcal{H} = \{h^*\}$ を学習アルゴリズムに提示するのが最もよい方法
しかし、そのような仮説 $h^*$ を見つけることが学習問題のもともとの目的

したがって単一のタスクのみを対象にしたメタ学習は通常の仮説の学習と等価であるといえます。

Baxterによる統計的メタ学習の提案

従来手法との違い

単一のタスクではなく、類似した複数のタスクを提示
それらタスク群に共通して適した帰納バイアスの獲得を目指す

統計的メタ学習問題：

学習アルゴリズムに対して仮説集合の集合 $\mathbb{H} = \{\mathcal{H}\}$ が提示される
アルゴリズムは与えられたタスク群に対してよい帰納バイアス
すなわち一つの仮説集合 $\mathcal{H} \in \mathbb{H}$ を見つけることを目的

単一学習問題の定式化（復習）

基本設定

入力空間：$\mathcal{X}$、出力空間：$\mathcal{Y}$

同時分布：$P_{X,Y} = P_{\mathcal{X} \times \mathcal{Y}}$ を $\mathcal{X} \times \mathcal{Y}$ 上の同時分布

仮説集合：$\mathcal{H} = \{h : \mathcal{X} \rightarrow \mathcal{Y}\}$

損失関数：$\ell : \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}$

学習の目的

仮説 $h \in \mathcal{H}$ で $\mathbf{x} \in \mathcal{X}$ の出力 $y \in \mathcal{Y}$ を予測
損失：$\mathcal{L}(\mathbf{x}, y; h) = \ell(h(\mathbf{x}), y)$
学習の目的は期待リスク $R(h) = \mathbb{E}_{(\mathbf{x}, y) \sim P_{X,Y}}[\mathcal{L}(\mathbf{x}, y; h)]$ を最小にするような仮説 $h \in \mathcal{H}$ を見つけること

学習アルゴリズムの定式化

定義3.20による学習アルゴリズム：

$n$個のラベルありデータ $D_n = \{(\mathbf{x}_i, y_i)\}_{i=1}^n \subset \mathcal{X} \times \mathcal{Y}$ を受け取りある仮説 $h \in \mathcal{H}$ を返す写像

$$A : \bigcup_{n=1}^{\infty} (\mathcal{X} \times \mathcal{Y})^n \rightarrow \mathcal{H} \quad (9.3)$$

経験リスク最小化

多くの学習問題は訓練データ $D_n$ 上の経験リスク $\hat{R}(h) = \frac{1}{n} \sum_{i=1}^n \mathcal{L}(\mathbf{x}_i, y_i; h)$ を最小化して仮説 $h$ を決定
学習アルゴリズムの記号 $A$ を用いて：

$$A(D_n) = \arg\min_{h \in \mathcal{H}} \hat{R}(h) \quad (9.4)$$

9.2.2 統計的メタ学習の定式化

9.2.2.1 メタ期待リスクとメタ経験リスク

タスク分布と環境の設定

タスクの定義

タスク：データの生成分布 $P_{X,Y}$ と損失 $\mathcal{L}$ の組 $\mathcal{T} = (P_{X,Y}, \mathcal{L})$

統計的メタ学習の設定

タスク集合 $\mathbb{T} = \{\mathcal{T}\}$ を考え、学習アルゴリズムに提示されるタスクは $\mathbb{T}$ 上の確率分布 $P(\mathcal{T})$ に従ってサンプリングされたものであると仮定
$P(\mathcal{T})$ はタスク分布（task distribution）と呼ばれる

環境（Environment）

環境：タスク集合 $\mathbb{T}$ とタスク分布 $P(\mathcal{T})$ の組 $(\mathbb{T}, P(\mathcal{T}))$

タスク分布 $P(\mathcal{T})$ は学習アルゴリズムにどのようなタスクが提示されやすいかを表します。

タスク分布の具体例

顔認識問題における帰納バイアス学習

目標：顔認識問題における帰納バイアスを学習したい

$P(\mathcal{T})$ として顔認識型の問題に対して高いピークを持つような確率分布を考える

対比例：文字認識問題における帰納バイアス学習

$P(\mathcal{T})$ として文字認識型の問題に対してピークを持つような確率分布を考える

メタ期待リスク（Meta-Expected Risk）

メタ期待リスク $\mathcal{R}(\mathcal{H})$ の定義：

$$\mathcal{R}(\mathcal{H}) = \mathbb{E}_{\mathcal{T} \sim P(\mathcal{T})} \left[ \inf_{h \in \mathcal{H}} R(h) \right] \quad (9.5)$$ $$= \mathbb{E}_{(P_{X,Y}, \mathcal{L}) \sim P(\mathcal{T})} \left[ \inf_{h \in \mathcal{H}} \mathbb{E}_{(\mathbf{x}, y) \sim P_{X,Y}} [\mathcal{L}(\mathbf{x}, y; h)] \right]$$

統計的メタ学習の目的

仮説集合の集合 $\mathbb{H} = \{ \mathcal{H}\}$ からメタ期待リスク（meta-expected risk）を最小にするような仮説集合 $\mathcal{H}$ を見つけること

メタ期待リスクの解釈

メタ期待リスク $\mathcal{R}(\mathcal{H})$ が小さくなるのは、タスク分布 $P(\mathcal{T})$ に従ってランダムにサンプリングされた任意のタスク $(P_{X,Y}, \mathcal{L})$ に対してよい仮説 $h$ が高い確率で $\mathcal{H}$ に含まれる場合
この意味で、$\mathcal{R}(\mathcal{H})$ は仮説集合 $\mathcal{H}$ が表す帰納バイアスが環境 $(\mathbb{T}, P(\mathcal{T}))$ にどれだけ適合しているかを測る指標であると解釈できる

通常の学習問題において期待リスクを直接最小化できないのと同様に、メタ期待リスクもタスク分布 $P(\mathcal{T})$ が未知であるために直接最小化することはできません。

メタ経験リスク（Meta-Empirical Risk）

メタ学習のデータ設定

タスク分布 $P(\mathcal{T})$ からランダムに $M$ 個のタスク $\mathcal{T}_{S_1} = (P_{X,Y}^{(S_1)}, \mathcal{L}^{(S_1)}), \ldots, \mathcal{T}_{S_M} = (P_{X,Y}^{(S_M)}, \mathcal{L}^{(S_M)})$ が得られている
さらに各タスクにおける生成分布 $P_{X,Y}^{(S_m)}$ からサイズ $n_m$ のデータ $D_{S_m} = \{(\mathbf{x}_i^{(S_m)}, y_i^{(S_m)})\}_{i=1}^{n_m}$ が得られている
$\mathcal{T}_{S_m}$ はソースタスク（source task）と呼ばれ、各タスクのデータ集合 $D_{S_m}$ は学習エピソード（learning episode）などと呼ばれる

メタ経験リスク $\hat{\mathcal{R}}(\mathcal{H})$ の定義：

$$\hat{\mathcal{R}}(\mathcal{H}) = \frac{1}{M} \sum_{m=1}^M \inf_{h \in \mathcal{H}} \hat{R}_{S_m}(h) \quad (9.6)$$ $$= \frac{1}{M} \sum_{m=1}^M \inf_{h \in \mathcal{H}} \sum_{i=1}^{n_m} \mathcal{L}^{(S_m)}(\mathbf{x}_i^{(S_m)}, y_i^{(S_m)}; h)$$

メタ経験リスクの特徴と課題

メタ経験リスクの性質

メタ経験リスク $\hat{\mathcal{R}}(\mathcal{H})$ は、仮説集合 $\mathcal{H}$ の関数を用いて各訓練データ集合 $D_{S_m}$ で達成可能な最良の経験リスクを平均したもの
各タスクの期待リスク $R(h)$ ではなく経験リスク $\hat{R}_{S_m}(h)$ の $\inf$ をとっている
メタ期待リスクの不偏推定量ではない

(9.6)のメタ経験リスクでメタ期待リスクを近似することの理論的な正当化は9.2.2.2節で説明します。

メタ学習アルゴリズム

通常の学習アルゴリズムと同様に、メタ学習アルゴリズム $A_{\text{meta}}$ は一般に $m$ 個のタスクにおけるデータ集合 $D_{S_m}$, $m = 1, 2, \ldots$ を入力すると、ある仮説集合を出力する写像

$$A_{\text{meta}} : \bigcup_{m=1}^{\infty} \bigcup_{n_m=1}^{\infty} (\mathcal{X}_{S_m} \times \mathcal{Y}_{S_m})^{n_m} \rightarrow \mathbb{H} \quad (9.7)$$

メタリスクの性質と最適化の課題

集合の包含関係と単調性

重要な性質：

$\mathcal{H} \subset \mathcal{H}'$ であるような二つの仮説集合 $\mathcal{H}$ と $\mathcal{H}'$ に対して：
$\mathcal{R}(\mathcal{H}') \leq \mathcal{R}(\mathcal{H})$
$\hat{\mathcal{R}}(\mathcal{H}') \leq \hat{\mathcal{R}}(\mathcal{H})$

単調性：

集合の包含関係によって引数である仮説集合の間に順序を定義するとき、$\mathcal{R}$ や $\hat{\mathcal{R}}$ はこの順序について単調減少関数

最適化の課題

もし $\mathbb{H}$ に含まれるすべての $\mathcal{H}$ に包含関係が成り立つならば、常に最大の要素数を持つ $\mathcal{H}$ が選択されることになります。一方、仮説集合の間に包含関係が成り立つかどうかは集合族 $\mathbb{H}$ のとり方に依存します。したがって、$\mathcal{R}(\mathcal{H})$ や $\hat{\mathcal{R}}(\mathcal{H})$ の最小化は、一般には「最大の $\mathcal{H}$ を選ぶ」という単純なものにはなりません。

この課題は、メタ学習において適切な仮説集合族 $\mathbb{H}$ の設計が重要であることを示しています。

9.2.2.2 メタ経験リスクによる近似の精度評価

定理9.3：メタ経験リスクの精度保証(目標)

定理9.3

$\mathcal{P}$ を $\mathcal{X} \times \mathcal{Y}$ 上の同時分布 $P_{XY}$ の集合（タスク集合）とし、$Q$ を $\mathcal{P}$ 上の確率分布（タスク分布）とします。また、タスク $P_m$, $m = 1, \ldots, M$ は $Q$ による $\mathcal{P}$ からのサンプルであり、各タスクのデータ $\{(\mathbf{x}_{m,i}, y_{m,i})\}_{i=1}^n$ は分布 $P_m$ により生成されているとします。さらに、$\mathbb{H}$ を許容的な仮説集合族とします。もしタスク数 $M$ およびサンプルサイズ $n$ に対してそれぞれ

$$M \geq \max \left\{ \frac{256}{\varepsilon^2} \log \frac{8C(\frac{\varepsilon}{32}, \mathcal{G}^*)}{\delta}, \frac{64}{\varepsilon^2} \right\} \quad (9.14)$$ $$n \geq \max \left\{ \frac{256}{n\varepsilon^2} \log \frac{8C(\frac{\varepsilon}{32}, \mathcal{G}_\ell^M)}{\delta}, \frac{64}{\varepsilon^2} \right\}$$

が成り立つならば、少なくとも $1 - \delta$ 以上の確率で、任意の $\mathcal{H} \in \mathbb{H}$ に対して、(9.9)である

$$\mathcal{R}(\mathcal{H}) \leq \hat{\mathcal{R}}(\mathcal{H}) + \varepsilon$$

が成り立ちます。ここで、$C(a, \mathcal{G}^*)$ および $C(a, \mathcal{G}_\ell^M)$ は，

$$C(a, \mathcal{G}^*) = \sup_Q N(\mathcal{G}^*, d_{\mathcal{G}^*}, a)$$ $$C(a, \mathcal{G}_\ell^M) = \sup_{P_1, \ldots, P_M} N(\mathcal{G}_\ell^M, d_{\mathcal{G}_\ell^M}, a)$$

で定まり、それぞれ $\mathcal{G}^*$ および $\mathcal{G}_\ell^M$ の、タスク分布 $Q$ およびタスク $P_1, \ldots, P_M$ に関する最悪ケースの被覆数を表します。

理論的準備：問題設定と仮説集合の制約

問題設定の簡単化と仮定

タスク集合 $\mathbb{T} = \{\mathcal{T} = (P_{X,Y}, \mathcal{L})\}$ において、損失関数 $\mathcal{L}$ はただ一つの関数 $\ell : \mathcal{Y} \times \mathcal{Y} \rightarrow [0, 1]$ を用いて $\mathcal{L}(\mathbf{x}, y; h) = \ell(h(\mathbf{x}), y)$ で定まっているとする。
$\mathbb{T}$ は同時分布 $P_{XY}$ の集合 $\mathcal{P}$ と同一視できる
タスク数を $M$、すべてのタスクでそれぞれ $n$ 個の教師ありデータが得られているとする

仮説の制約

仮説 $h$ として、入力 $\mathbf{x} \in \mathcal{X}$ とパラメータ $\mathbf{w} \in \mathbb{R}^D$ を引数にとり、$[0, 1]$ に値をとる関数を考える。

$h : \mathcal{X} \times \mathbb{R}^D \rightarrow [0, 1]$ を考え、仮説集合 $\mathcal{H}$ は

$$\mathcal{H} = \{h(\cdot, \mathbf{w}) : \mathbf{w} \in \mathbb{R}^D\} \quad (9.8)$$

を扱う

仮説集合の許容性

定義9.1（仮説集合の許容性）

(9.8)で定まる仮説集合 $\mathcal{H}$ が許容的（permissible）であるとは、$h \in \mathcal{H}$ が $\mathcal{X}$ と $\mathbb{R}^D$ のボレル集合族の直積 $B(\mathcal{X}) \times B(\mathbb{R}^D)$ で定まる $\sigma$ 集合族に関して可測であること

数学的準備：関数集合の定義

関数集合 $\mathcal{H}_\ell$ と $\mathcal{H}_\ell^M$ の定義

仮説集合 $\mathcal{H} \in \mathbb{H}$ と損失関数 $\ell$ に対して、$\mathcal{H}_\ell = \{\ell \circ h; h \in \mathcal{H}\}$ とおく

$\mathcal{H}_\ell$ の元は仮説 $h \in \mathcal{H}$ と損失関数 $\ell$ の合成関数であり、任意の $(\mathbf{x}, y) \in \mathcal{X} \times \mathcal{Y}$ に対して $\ell(h(\mathbf{x}), y)$ で定まる

$M$ 個の仮説の平均損失関数

$M$ 個の仮説 $h_1, \ldots, h_M \in \mathcal{H}$ に対して、関数 $\bar{h}_\ell : (\mathcal{X} \times \mathcal{Y})^M \rightarrow [0, 1]$ を

$$\bar{h}_\ell(\{(\mathbf{x}_m, y_m)\}_{m=1}^M) = \frac{1}{M} \sum_{m=1}^M \ell(h_m(\mathbf{x}_m), y_m)$$

で定め、$\mathcal{H}_\ell^M = \{\bar{h}_\ell; h_1, \ldots, h_M \in \mathcal{H}\}$ とおく

データ点をそれぞれ別々の仮説で評価した損失の算術平均

関数集合 $\mathcal{G}_\ell^M$ の定義

$$\mathcal{G}_\ell^M = \bigcup_{\mathcal{H} \in \mathbb{H}} \mathcal{H}_\ell^M \quad (9.10)$$

期待リスクを返す関数集合 $\mathcal{G}^*$ の定義

$H^*$ 関数の定義

$\mathcal{H} \in \mathbb{H}$ に対して関数 $H^* : \mathcal{P} \rightarrow [0, 1]$ を

$$H^*(P_{XY}; \mathcal{H}) = \inf_{h \in \mathcal{H}} R_{P_{XY}}(h)$$ $$= \inf_{h \in \mathcal{H}} \mathbb{E}_{(\mathbf{x}, y) \sim P_{XY}} [\ell(h(\mathbf{x}), y)]$$

関数集合 $\mathcal{G}^*$ の定義

$$\mathcal{G}^* = \{H^*(\cdot; \mathcal{H}); \mathcal{H} \in \mathbb{H}\} \quad (9.11)$$

$\mathcal{G}^*$ の元は、各タスク（すなわちデータ生成分布）$P_{XY}$ に対して、$\mathcal{H}$ に含まれる仮説を用いたときの最小の期待リスクを返す関数になっています。

関数集合上の距離尺度

$\mathcal{G}_\ell^M$ 上の距離 $d_{\mathcal{G}_\ell^M}$

$P_1, \ldots, P_M \in \mathcal{P}$ を $\mathcal{X} \times \mathcal{Y}$ 上の同時分布の列とし、任意の $\bar{h}_\ell, \bar{h}_\ell' \in \mathcal{G}_\ell^M$ に対して

$$d_{\mathcal{G}_\ell^M}(\bar{h}_\ell, \bar{h}_\ell') = \int |\bar{h}_\ell(\{(\mathbf{x}_m, y_m)\}_{m=1}^M) - \bar{h}_\ell'(\{(\mathbf{x}_m, y_m)\}_{m=1}^M)|$$ $$dP_1(\mathbf{x}_1, y_1) \cdots dP_M(\mathbf{x}_M, y_M) \quad (9.12)$$

$\mathcal{G}^$ 上の距離 $d_{\mathcal{G}^}$

$\mathcal{P}$ 上の任意の分布（すなわちタスク分布）$Q$ と任意の $H_1^*, H_2^* \in \mathcal{G}^*$ に対して，

$$d_{\mathcal{G}^*}(H_1^*, H_2^*) = \int |H_1^*(P) - H_2^*(P)| dQ(P) \quad (9.13)$$

これらの距離は定義から非負であり、対称性と三角不等式を満たします。また、$d_{\mathcal{G}_\ell^M}$ と $d_{\mathcal{G}^*}$ はそれぞれ $\mathcal{G}_\ell^M$ および $\mathcal{G}^*$ 上の擬距離です。

被覆数（Covering Number）

定義9.2（$\mathcal{G}_\ell^M$ の被覆数）

$\mathcal{F}$ を $\mathcal{G}_\ell^M$ の部分集合とし、$\varepsilon > 0$ とします。任意の $\bar{h}_\ell \in \mathcal{G}_\ell^M$ に対して、ある $\bar{h}_\ell' \in \mathcal{F}$ が存在して、$d_{\mathcal{G}_\ell^M}(\bar{h}_\ell, \bar{h}_\ell') < \varepsilon$ を満たすとき、$\mathcal{F}$ を $\mathcal{G}_\ell^M$ の $\varepsilon$-ネットと呼びます。$\mathcal{G}_\ell^M$ の $\varepsilon$-ネットが達成しうる最小の要素数を、$\mathcal{G}_\ell^M$ の被覆数と呼び、$N(\mathcal{G}_\ell^M, d_{\mathcal{G}_\ell^M}, \varepsilon)$ と書きます。すなわち，

$$N(\mathcal{G}_\ell^M, d_{\mathcal{G}_\ell^M}, \varepsilon) = \min_{\mathcal{F}: \mathcal{G}_\ell^M \text{の} \varepsilon\text{-ネット}} |\mathcal{F}|$$

図9.2：$\varepsilon$-ネットのイメージ

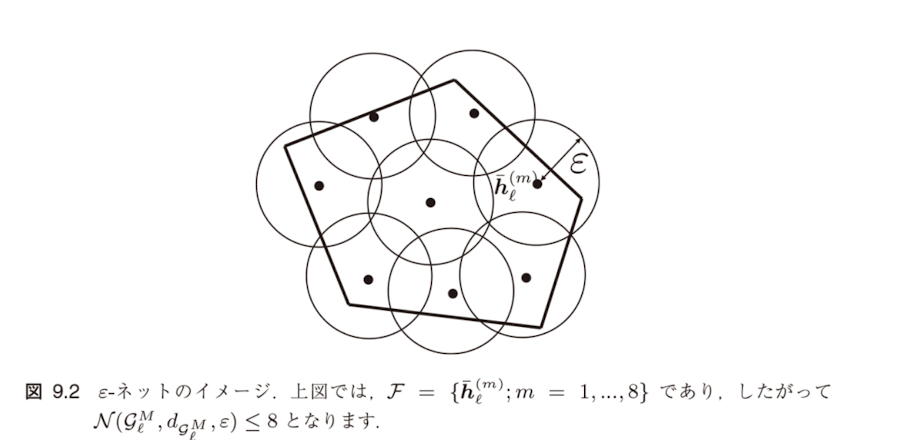
上図では、$\mathcal{F} = \{\bar{h}_\ell^{(m)}; m = 1, \ldots, 8\}$ であり、したがって $N(\mathcal{G}_\ell^M, d_{\mathcal{G}_\ell^M}, \varepsilon) \leq 8$ となります。

$\mathcal{G}^*$ に対する被覆数 $N(\mathcal{G}^*, d_{\mathcal{G}^*}, \varepsilon)$ も同様に定義されます。

定理9.3：メタ経験リスクの精度保証

定理9.3

$\mathcal{P}$ を $\mathcal{X} \times \mathcal{Y}$ 上の同時分布 $P_{XY}$ の集合（タスク集合）とし、$Q$ を $\mathcal{P}$ 上の確率分布（タスク分布）とします。また、タスク $P_m$, $m = 1, \ldots, M$ は $Q$ による $\mathcal{P}$ からのサンプルであり、各タスクのデータ $\{(\mathbf{x}_{m,i}, y_{m,i})\}_{i=1}^n$ は分布 $P_m$ により生成されているとします。さらに、$\mathbb{H}$ を許容的な仮説集合族とします。もしタスク数 $M$ およびサンプルサイズ $n$ に対してそれぞれ

$$M \geq \max \left\{ \frac{256}{\varepsilon^2} \log \frac{8C(\frac{\varepsilon}{32}, \mathcal{G}^*)}{\delta}, \frac{64}{\varepsilon^2} \right\} \quad (9.14)$$ $$n \geq \max \left\{ \frac{256}{n\varepsilon^2} \log \frac{8C(\frac{\varepsilon}{32}, \mathcal{G}_\ell^M)}{\delta}, \frac{64}{\varepsilon^2} \right\}$$

が成り立つならば、少なくとも $1 - \delta$ 以上の確率で、任意の $\mathcal{H} \in \mathbb{H}$ に対して、(9.9)である

$$\mathcal{R}(\mathcal{H}) \leq \hat{\mathcal{R}}(\mathcal{H}) + \varepsilon$$

が成り立ちます。ここで、$C(a, \mathcal{G}^*)$ および $C(a, \mathcal{G}_\ell^M)$ は，

$$C(a, \mathcal{G}^*) = \sup_Q N(\mathcal{G}^*, d_{\mathcal{G}^*}, a)$$ $$C(a, \mathcal{G}_\ell^M) = \sup_{P_1, \ldots, P_M} N(\mathcal{G}_\ell^M, d_{\mathcal{G}_\ell^M}, a)$$

で定まり、それぞれ $\mathcal{G}^*$ および $\mathcal{G}_\ell^M$ の、タスク分布 $Q$ およびタスク $P_1, \ldots, P_M$ に関する最悪ケースの被覆数を表します。

定理9.3の意義と実用性

定理の主張

(9.9)において、$\mathcal{R}$ と $\hat{\mathcal{R}}$ が近いことを保証するためのタスク数 $M$ とサンプルサイズ $n$ が、導入した関数集合 $\mathcal{G}_\ell^M$ および $\mathcal{G}^*$ の被覆数によって制約されることを主張するものです。

歴史的背景と現代的意義

定理9.3が発表されたのは2000年であり、まだ深層学習が爆発的な発展を見せる以前の研究
現在の深層ニューラルネットワークモデルの大規模化に通じる解釈を与えることができる

理論的意義

タスク数 $M$ とサンプルサイズ $n$ が条件(9.14)を満たす範囲において、理論的保証を提供
被覆数による複雑性の制御

実用上の課題

大規模モデルでは被覆数の計算が困難
現実的な設定での適用可能性の限界

定理の中で明示的に扱われていませんが、被覆数を測る指標である被覆リソース解放を明示的にする時間や複雑さについて、タスク数 $M$ とサンプルサイズ $n$ および被覆リソース解放によって制約条件が課されることを明示しています。

深層学習モデルへの応用と解釈

現代的な解釈

仮説集合の許容性：$h$ の可測性は、$T$ が完備かつ可分な距離空間（と同様な空間）の部分集合であることを要請
$\mathbb{R}^D$ は自身が完備かつ可分な距離空間であるため、この性質は満たされている

大規模モデルでの考察

パラメータ空間の巨大化

大規模ニューラルネットワークでは $D$ が極めて大きい
モデルのサイズ $D$（および計算リソース）を膨大化させる

理論と実践のギャップ

理論的には経験リスクによる期待リスクの近似について、タスク数 $M$ とサンプルサイズ $n$ および被覆リソースが重要
しかし実際にはこれらの指標関係についていくらか緩い制約で実現されている

この解釈は、深層ニューラルネットワークをモデルの大規模化に対する理論的説明の一つであるベき定理 [159] に通じるものがあります。すなわち、モデルパラメータ数、データ数などのリソース指標、および計算力について、三つの指標の組み合わせによって機能的結果を実現することを合理的に解釈する考え方に通じています。

理論的保証を得た上で、実際のメタ学習アルゴリズムをどのように実装・評価するかが次の話題です。

9.2.2.3 メタ訓練とメタテスト

メタ訓練（Meta-Training）フェーズ

メタ訓練の目的

メタ経験リスク（9.6）を最小化して仮説集合を学習するステップ

メタ訓練の定式化：

$$\hat{\mathcal{H}} = \arg\min_{\mathcal{H} \in \mathbb{H}} \hat{\mathcal{R}}(\mathcal{H}) \quad (9.15)$$

ここで、メタ経験リスク $\hat{\mathcal{R}}(\mathcal{H})$ は：

$$\hat{\mathcal{R}}(\mathcal{H}) = \frac{1}{M} \sum_{m=1}^M \inf_{h \in \mathcal{H}} \hat{R}_{S_m}(h) \quad (9.6)$$

メタ訓練の具体的手順

ステップ1：$M$ 個のソースタスクとそれぞれのデータを収集

ステップ2：仮説集合の候補 $\mathbb{H} = \{\mathcal{H}\}$ を設定

ステップ3：各仮説集合 $\mathcal{H} \in \mathbb{H}$ に対してメタ経験リスク $\hat{\mathcal{R}}(\mathcal{H})$ を計算

ステップ4：最小のメタ経験リスクを持つ仮説集合 $\hat{\mathcal{H}}$ を選択

メタテスト（Meta-Testing）フェーズ

メタテストの目的

メタ訓練で学習された仮説集合 $\hat{\mathcal{H}}$ の性能を新しいタスクで検証する

メタテストの詳細手順

1. テストタスクの準備

$Q$ 個のテストタスク $\mathcal{T}_{T_q} = \{P_{X,Y}^{(T_q)}, \mathcal{L}^{(T_q)}\} \sim P(\mathcal{T})$, $q = 1, \ldots, Q$ を用意

2. データの分割

各タスクにおける生成分布から得られたデータ $D_{T_q} \sim P_{X,Y}^{(T_q)}$ を以下に分割：

訓練集合 $D_{T_q}^{\text{tr}}$：仮説学習用
テスト集合 $D_{T_q}^{\text{te}}$：性能評価用

3. 仮説の学習

$D_{T_q}^{\text{tr}}$ に対して通常の仮説の学習問題を解く

メタテストにおける仮説学習

個別タスクでの学習問題

各テストタスク $q$ に対する学習問題：

$$\min_{h \in \hat{\mathcal{H}}} R_{T_q}(h) = \frac{1}{|D_{T_q}^{\text{tr}}|} \sum_{(\mathbf{x}, y) \in D_{T_q}^{\text{tr}}} \mathcal{L}^{(T_q)}(\mathbf{x}, y; h) \quad (9.16)$$

この最適化により仮説 $\hat{h}_{T_q}$ を得る

性能評価

評価指標

$\hat{h}_{T_q}$ の性能をテストデータ $D_{T_q}^{\text{te}}$ で評価
複数のテストタスクでの平均性能
学習効率（少ないデータでの性能向上）

評価の意義

メタ訓練で得られた $\hat{\mathcal{H}}$ の質を測定
新タスクへの適応速度を評価
帰納バイアスの有効性を検証

メタ学習の最終目標

メタ訓練で得られた $\hat{\mathcal{H}}$ がどれくらいよい帰納バイアスなのかが評価される

メタ学習のワークフロー全体

完全なメタ学習プロセス

メタ訓練段階

入力：$M$ 個のソースタスク
各タスクのデータ $D_{S_m}$

処理：メタ経験リスク最小化
$\hat{\mathcal{H}} = \arg\min \hat{\mathcal{R}}(\mathcal{H})$

出力：最適仮説集合 $\hat{\mathcal{H}}$

→

メタテスト段階

入力：$Q$ 個のテストタスク
学習済み仮説集合 $\hat{\mathcal{H}}$

処理：各タスクで個別学習
$\hat{h}_{T_q} = \arg\min R_{T_q}(h)$

出力：各タスクでの性能評価
メタ学習の効果測定

このワークフローは現在のfew-shot learning、domain adaptation、neural architecture searchなどの実用的なメタ学習手法の基盤となっています。

9.2.3 より一般的なメタ学習の定式化

メタ知識（Meta-knowledge）の導入

メタ知識 $\omega$ の定義

メタ学習の学習対象を一般にメタ知識（meta-knowledge）と呼び、パラメータ $\omega$ で表すことにします

メタ知識の具体例

ニューラルネットワークのパラメータの初期値
学習に用いるオプティマイザの種類や設定
仮説集合 $\mathcal{H}$（従来のBaxterのアプローチ）
ハイパーパラメータの最適値

一般化されたメタ期待リスク

タスク $\mathcal{T} = (P_{X,Y}, \mathcal{L})$ においてメタ知識 $\omega$ を用いたときの損失を記号 $\mathcal{L}(\omega; P_{X,Y})$ で表すことにすると、$\omega$ の学習は (9.5) のメタ期待リスク $\mathcal{R}(\mathcal{H})$ を一般化した

$$\mathcal{R}(\omega) = \mathbb{E}_{\mathcal{T} \sim P(\mathcal{T})}[\mathcal{L}(\omega; P_{X,Y})] \quad (9.17)$$

を $\omega$ について最小化することで行われます。

メタ経験リスクの一般化

一般化されたメタ経験リスク

損失 $\mathcal{L}(\omega; P_{X,Y})$ は、メタ知識 $\omega$ のもとでデータ $D \sim P_{X,Y}$ から学習されたモデルの性能を表します。

$\mathcal{T}_{S_1} = (P_{X,Y}^{(S_1)}, \mathcal{L}^{(S_1)}), \ldots, \mathcal{T}_{S_M} = (P_{X,Y}^{(S_M)}, \mathcal{L}^{(S_M)})$ をタスク分布 $P(\mathcal{T})$ からランダムに得られた $M$ 個のタスクとしたとき、$\mathcal{R}(\omega)$ は (9.6) のメタ経験リスク $\hat{\mathcal{R}}(\mathcal{H})$ の一般化

$$\hat{\mathcal{R}}(\omega) = \frac{1}{M} \sum_{m=1}^M \mathcal{L}^{(S_m)}(\omega; P_{X,Y}^{(S_m)}) \quad (9.18)$$

によって近似されます。

メタ学習のプロセス

メタ訓練

$\hat{\mathcal{R}}(\omega)$ を最小化してメタ知識の推定値 $\hat{\omega}$ を得る
複数のソースタスクから共通の知識を抽出

メタテスト

テストタスク $\mathcal{T}_{T_q} = \{P_{X,Y}^{(T_q)}, \mathcal{L}^{(T_q)}\}, q = 1, \ldots, Q$ のデータ $D_{T_q} = \{D_{T_q}^{\text{tr}}, D_{T_q}^{\text{te}}\} \sim P_{X,Y}^{(T_q)}$ を用いて $\hat{\omega}$ の性能を検証

メタテストにおける性能評価

メタテストの手順

各テストタスク $q = 1, \ldots, Q$ に対して：

$$\min_{h \in \mathcal{H}} \hat{R}_{T_q}(h) = \frac{1}{|D_{T_q}^{\text{tr}}|} \sum_{(\mathbf{x}, y) \in D_{T_q}^{\text{tr}}} \mathcal{L}^{(T_q)}(\omega; P_{X,Y}^{(T_q)}) \quad (9.19)$$

を解いて仮説 $\hat{h}_{T_q}$ を学習し、$D_{T_q}^{\text{te}}$ から計算されるテスト誤差によって $\hat{\omega}$ の性能を検証します。

帰納バイアス学習のためのメタ学習と同様、まずメタ訓練ステップで $\hat{\mathcal{R}}(\omega)$ を最小化してメタ知識の推定値 $\hat{\omega}$ を得ます。次にメタテストステップでテストタスクのデータを用いて $\hat{\omega}$ の性能を検証します。

例9.1：ハイパーパラメータ最適化への応用

例9.1（機械学習モデルのハイパーパラメータ最適化）

メタ学習を上述のように定式化すると、例えば従来の機械学習におけるモデルのハイパーパラメータ最適化をメタ学習として解釈することができます。

K重交差検証法による最適化

5.1.2.1節で説明したK重交差検証法によるハイパーパラメータ最適化を考える
データ集合 $D$ を $K$ 分割し、$K$ 組の訓練、検証データ集合 $\{D_k^{\text{tr}}, D_k^{\text{val}}\}$, $k = 1, \ldots, K$ を作る
各 $\{D_k^{\text{tr}}, D_k^{\text{val}}\}$ がメタ学習における一つのタスクに相当

仮説とパラメータの設定

モデルパラメータ $\theta$ およびハイパーパラメータ $\omega$ を持つ仮説を $h_{\theta,\omega}$ と書くとき、K重交差検証法は、以下の最適化問題として定式化されます：

K重交差検証の数学的定式化

K重交差検証の最適化問題：

$$\min_\omega \frac{1}{K} \sum_{k=1}^K \frac{1}{|D_k^{\text{val}}|} \sum_{(\mathbf{x}, y) \in D_k^{\text{val}}} \mathcal{L}(\mathbf{x}, y; h_{\hat{\theta}_k, \omega})$$ $$\text{subject to } \hat{\theta}_k = \arg\min_\theta \frac{1}{|D_k^{\text{tr}}|} \sum_{(\mathbf{x}, y) \in D_k^{\text{tr}}} \mathcal{L}(\mathbf{x}, y; h_{\theta, \omega}), \quad k = 1, 2, \ldots, K$$

(9.20)

式の解釈

目的関数（1行目）

あるハイパーパラメータ値 $\omega$ のもとで各タスクの個別の学習（2行目）で得られたモデルパラメータ $\hat{\theta}_k$ を用いたときの検証誤差

制約条件（2行目）

各分割 $k$ において訓練データ $D_k^{\text{tr}}$ を用いてモデルパラメータ $\theta$ を最適化
ハイパーパラメータ $\omega$ は固定

ここで、(9.20)の目的関数（1行目）は、あるハイパーパラメータ値 $\omega$ のもとで各タスクの個別の学習（2行目）で得られたモデルパラメータ $\hat{\theta}_k$ を用いたときの検証誤差を表します。

9.2.4 メタ知識の学習

9.2.4.1 2レベル最適化による学習の定式化

一般的な2レベル最適化問題の定式化

メタ学習の2レベル最適化問題：

$$\min_\omega \sum_{m=1}^M \mathcal{L}^{\text{meta}}(\hat{\theta}_m(\omega), \omega, D_{S_m}^{\text{val}}) \quad (9.21)$$ $$\text{subject to } \hat{\theta}_m(\omega) = \arg\min_\theta \mathcal{L}^{(S_m)}(\theta, \omega, D_{S_m}^{\text{tr}}), \quad m = 1, \ldots, M$$

記号の意味

各タスクの訓練データ $D_{S_m}^{\text{tr}}$ と検証データ $D_{S_m}^{\text{val}}$ はそれぞれサポート集合（support set）、クエリ集合（query set）とも呼ばれる
(9.21)の制約条件である個別のタスクの学習問題をベース学習（base learning）フェーズと呼ぶ

2レベル最適化の流れ

まずメタ知識 $\omega$ の初期条件を適当に与え、$\omega$ のもとでベース学習によって各タスクの個別のモデルパラメータ $\hat{\theta}_m(\omega)$ を学習
次に、$\hat{\theta}_m(\omega), m = 1, \ldots, M$ を用いて $\omega$ のよさをメタ損失 $\mathcal{L}^{\text{meta}}$ で評価し、これを更新

メタ学習フェーズとベース学習フェーズの非対称性

重要な特徴

非対称性による制約

メタ損失の記号 $\mathcal{L}^{\text{meta}}$ は内部ループであるベース学習の損失 $\mathcal{L}^{(S_m)}$ と区別し外部ループの損失であることを明示するために用いているものですが、メタ損失自体は基本的にベース学習の損失と同じ損失関数によって評価されます

具体例

分類タスクのとき：交差エントロピー損失
回帰タスクのとき：二乗損失など

2レベル最適化の主な特徴

メタ学習フェーズとベース学習フェーズの非対称性にあるといえます。具体的にいうと、(9.21)の制約条件であるベース学習フェーズはメタ学習フェーズで得られたメタ知識 $\omega$ をパラメータとして含みますが、ベース学習中にこの $\omega$ を変更することはできません。

2レベル最適化が可能な $\omega$ の例

具体的な応用例

非凸最適化の初期条件[96]
正則化の強さを制御するハイパーパラメータ[99]
目標タスクの損失関数 $\mathcal{L}$ のパラメータ化の方法[180]

これらはすべて、メタ学習において学習可能な対象として扱うことができ、2レベル最適化の枠組みで最適化することが可能です。

9.2.4.2 線形回帰タスクの環境におけるメタ知識の学習の例

線形回帰におけるメタ学習の設定

問題設定

環境 $(\mathbb{T}, P(\mathcal{T}))$ が線形回帰の空間として与えられる場合を例として取り上げ、(9.21)で抽象的に定義されたメタ知識の学習が具体的にどう実現されるのかを説明します

線形回帰の数学的設定

いま、$\mathcal{X} = \mathbb{R}^d$、$\mathcal{Y} = \mathbb{R}$ とし、タスク $\mathcal{T} = (P_{X,Y}, \mathcal{L}) \sim P(\mathcal{T})$ は、データ生成分布 $P_{X,Y}$ が

$$(\mathbf{x}, y) \sim P_{X,Y} \Leftrightarrow \mathbf{x} \sim P_X, \quad \varepsilon \sim \eta, \quad y = \boldsymbol{\theta}^{\top} \mathbf{x} + \varepsilon \quad (9.22)$$

となるような周辺分布 $P_X$、ノイズ分布 $\eta$ および線形モデルのパラメータ $\boldsymbol{\theta}$ の三つ組 $(P_X, \eta, \boldsymbol{\theta})$ で定まるとします。また、損失 $\mathcal{L}$ は二乗損失 $\mathcal{L}(\mathbf{x}, y; h) = (h(\mathbf{x}) - y)^2$ で与えられるものとします。

リッジ回帰によるメタ学習

メタ知識の設定

このとき、Denevi ら [75] は線形モデルのパラメータ $\boldsymbol{\theta}$ を学習するためのアルゴリズム $\mathcal{A}_\omega : D_n = \{(\mathbf{x}_i, y_i)\}_{i=1}^n \mapsto \hat{\boldsymbol{\theta}}(D_n; \omega)$ として以下のようなリッジ回帰型の最適化問題を考察しました

$$\mathcal{A}_\omega(D_n) = \hat{\boldsymbol{\theta}}(D_n; \omega) = \arg\min_{\boldsymbol{\theta} \in \mathbb{R}^d} \frac{1}{n} \|\mathbf{X}\boldsymbol{\theta} - \mathbf{y}\|^2 + \lambda\|\boldsymbol{\theta} - \boldsymbol{\omega}\|^2 \quad (9.23)$$

記号の説明

$\mathbf{X} = (\mathbf{x}_1^{\top}, \ldots, \mathbf{x}_n^{\top})$ は計画行列
$\mathbf{y} = (y_1, \ldots, y_n)^{\top}$ は出力ベクトル
ベクトル $\boldsymbol{\omega} \in \mathbb{R}^d$ は線形回帰の環境において各タスクのモデルパラメータ $\boldsymbol{\theta}$ に共通して近い、平均ベクトルのような役割を持つメタ知識を表す

メタ知識 $\boldsymbol{\omega}$ は環境中のタスク間の類似度を表現するベクトルであり、$\boldsymbol{\omega}$ を推定できれば、同一の環境における新たなタスクに対する効率的な適応が期待できます。

リッジ回帰におけるメタ期待リスクとメタ経験リスク

メタ期待リスクの導出

リッジ回帰 (9.23) におけるメタ知識 $\boldsymbol{\omega}$ の学習は、メタ期待リスク

$$\mathcal{R}(\boldsymbol{\omega}) = \mathbb{E}_{\mathcal{T} \sim P(\mathcal{T})} \left[ \mathbb{E}_{D_n \sim P_{X,Y}} \left[ \mathbb{E}_{(\mathbf{x}, y) \sim P_{X,Y}} \left[ \frac{1}{2} \left( (\hat{\boldsymbol{\theta}}(D_n; \boldsymbol{\omega}))^{\top} \mathbf{x} - y \right)^2 \right] \right] \right] \quad (9.24)$$

を $\boldsymbol{\omega}$ について最小化する問題として定義できます。

解析的解の導出

リッジ回帰 (9.23) のモデルパラメータ $\hat{\boldsymbol{\theta}}(D_n; \boldsymbol{\omega})$ が、$C = \frac{1}{n}\mathbf{X}^{\top}\mathbf{X} + \lambda I$ として $\hat{\boldsymbol{\theta}}(D_n; \boldsymbol{\omega}) = C^{-1}(\frac{1}{n}\mathbf{X}^{\top} \mathbf{y} + \lambda\boldsymbol{\omega})$ と解析的に書けることから、メタ期待リスク $\mathcal{R}(\boldsymbol{\omega})$ は以下のように書き換えることができます (Denevi ら [75] の Proposition 1)。

$$\mathcal{R}(\boldsymbol{\omega}) = \frac{1}{2} \mathbb{E}_{\mathbf{x}, \tilde{y}} \left[ (\boldsymbol{\omega}^{\top} \tilde{\mathbf{x}} - \tilde{y})^2 \right] \quad (9.25)$$

ここで、$\tilde{\mathbf{x}} = \lambda C^{-1} \mathbf{x}$、$\tilde{y} = y - \frac{1}{\lambda n} (\mathbf{X}^{\top} \mathbf{y})^{\top} \tilde{\mathbf{x}}$ とおきました。

メタ経験リスクによる近似

メタ経験リスクの定義

(9.25)の $\mathcal{R}(\boldsymbol{\omega})$ はメタ経験リスク

$$\hat{\mathcal{R}}(\boldsymbol{\omega}) = \frac{1}{2m} \sum_{j=1}^m (\boldsymbol{\omega}^{\top} \tilde{\mathbf{x}}_j^{\text{val}} - \tilde{y}_j^{\text{val}})^2 \quad (9.26)$$

によって近似されます。ここで、$\tilde{\mathbf{x}}_j^{\text{val}}$ および $\tilde{y}_j^{\text{val}}$ は $\{(\mathbf{x}_j^{\text{val}}, y_j^{\text{val}})\}$ を訓練データと異なる検証データとして (9.25) の $\tilde{\mathbf{x}}, \tilde{y}$ と同様に計算されるものです。

実装の詳細

メタ経験リスク $\hat{\mathcal{R}}(\boldsymbol{\omega})$ の最小化は、次のような2ステップの反復アルゴリズムで実行することができます (Denevi ら [75] の Algorithm 1)。

Deneviらのアルゴリズム

Step1（ベース学習フェーズ）

データ $D_n$ を受け取り、サイズ $n - m$ の訓練データ $D^{\text{tr}}$ とサイズ $m$ の検証データ $D^{\text{val}}$ に分割して $\tilde{\mathbf{x}}_j^{\text{val}}, \tilde{y}_j^{\text{val}}, j = 1, \ldots, m$ を以下で計算します。

$$\tilde{\mathbf{x}}_j^{\text{val}} \leftarrow \lambda C^{-1} \mathbf{x}_j^{\text{val}} \quad (9.27)$$ $$\tilde{y}_j^{\text{val}} \leftarrow y_j^{\text{val}} - \frac{1}{\lambda n} (\mathbf{X}^{\text{tr}\top} \mathbf{y}^{\text{tr}})^{\top} \tilde{\mathbf{x}}_j^{\text{val}}$$

Step2（メタ学習フェーズ）

メタ経験リスク $\hat{\mathcal{R}}(\boldsymbol{\omega})$ の勾配 $\nabla_{\boldsymbol{\omega}} \hat{\mathcal{R}}(\boldsymbol{\omega})$ を計算し、

$$\boldsymbol{\omega} \leftarrow \boldsymbol{\omega} - \gamma \nabla_{\boldsymbol{\omega}} \hat{\mathcal{R}}(\boldsymbol{\omega}) \quad (9.28)$$

でメタ知識 $\boldsymbol{\omega}$ を更新します。

実際には、各反復におけるメタ知識 $\boldsymbol{\omega}$ をすべて記憶しておき、それらの標本平均をメタ知識の推定値として出力します。

モデルベースメタ学習への発展

一般化の方向性

メタ学習の実現方法

以上のようなメタ学習の実現は、メタ知識 $\boldsymbol{\omega}$ の学習であると同時に、(9.23)のような写像 $\mathcal{A}_\omega$ の学習と捉えることもできます

より一般的なアプローチ

(9.23)でリッジ回帰として定義されていた $\mathcal{A}_\omega$ を一般化
サポート集合 $D_n$ を入力してベースタスクのモデルパラメータ $\boldsymbol{\theta}$ を出力する写像 $\mathcal{A} : D \mapsto \boldsymbol{\theta} = \mathcal{A}(D_n)$ を考え
これをニューラルネットワークなどの適切なモデルで近似 [111]

9.3 メタ学習の分類と方法

9.3.1 メタ学習の分類の概要

メタ学習の分類の概要

メタ学習は3つの軸で分類されます

メタ目的（meta-objective）：何をメタ学習の目標とするか
メタオプティマイザ（meta-optimizer）：どのようにメタ知識を更新するか
メタ表現（meta-representation）：何をメタ知識として扱うか

Hospedales等による分類 [139] では、これらの3つの軸でメタ学習の様々な手法を体系化しています。

メタ目的による分類

メタ学習の目標設定

分類軸	内容	例
少数ショット vs 多数ショット	目標ドメインの利用可能なデータ量	Few-shot learning, Full-shot learning
シングルタスク vs マルチタスク	適応対象のタスク数	単一目標ドメイン、多目標ドメイン
オンライン vs オフライン	メタ知識の更新タイミング	継続的学習、事前学習

目標設定によってメタ学習のアプローチが大きく変わります。

メタオプティマイザによる分類

外部ループであるメタ知識の学習で用される最適化アルゴリズムの種類(どう転移するか)

メタ知識の更新方法

勾配法による更新

メタ損失関数の $\omega$ に関する勾配 $\mathcal{L}^{\text{meta}}/\partial \omega$ を利用

典型的な勾配更新式：

$\omega$ はモデルパラメータ $\theta$ を介して $\mathcal{L}^{\text{meta}}$ に寄与

勾配：$(\partial \mathcal{L}^{\text{meta}}/\partial \theta)(\partial \theta/\partial \omega)$

解析的勾配を利用するため効率的ですが、計算コストが高くなる場合があります。

勾配法以外のメタオプティマイザ

進化的探索による更新

進化的探索の利点

微分可能性の制約を受けない：任意のベースモデルとメタ損失を最適化可能
誤差逆伝搬不要：勾配劣化問題や従来手法の高次勾配計算コストを回避
並列化可能：スケーラビリティが高い
多様性の確保：局所解を回避しやすい

一方で、収束まで長時間を要し、理論的性質の解析が困難な場合が多い。

メタ表現による分類

メタ知識として何を学習するか（何を転移するか）

メタ表現の種類

「何をメタ学習の対象 = メタ知識とするのか」という観点による分類

モデルパラメータの初期値
モデルの最適化手法

9.3.2 メタ知識の表現に基づく分類と方法

メタ知識の表現とは

メタ知識 $\omega$ として何を考えるか

学習戦略のどの部分をメタ学習の対象とし、どの部分を対象としないか（ユーザが与える固定戦略とするか）を決めること

主なメタ知識の種類

メタ知識の種類	内容	文献
仮説集合	$\mathcal{H} = \{h_\theta \| \theta \in \Theta\}$	9.2.2節
パラメータ初期値	$h_\theta$ を規定するパラメータ $\theta$ の初期化	[96]
ハイパーパラメータ	モデルの設定や学習率など	[23, 99]
ブラックボックスモデル	サポート集合→ベースタスクモデルパラメータ	9.2.4.2節

アーキテクチャもメタ知識となる

ニューラルネットワークのアーキテクチャ構造

仮説がニューラルネットワークの場合、アーキテクチャの構成も学習の対象となります

メタ学習におけるオプティマイザの学習

通常の機械学習：SGD、Adamなど既存のオプティマイザを利用
メタ学習における革新的アプローチ：

オプティマイザ自体をメタ知識として学習

反復 $t$ における現在のパラメータ値 $\theta_t$
損失の勾配 $\nabla_\theta \mathcal{L}(\theta_t)$ を入力
反復におけるパラメータ更新を出力する写像を学習

このアプローチにより、タスクに特化したオプティマイザを獲得できます [60, 239, 276]。

データもメタ知識の対象

学習データの生成・拡張

データ拡張手法

学習用サポート集合
データ拡張 [65]
ミニバッチの切り分け方 [192]

環境シミュレータ

Sim2Real転移
環境のシミュレータ [13]
データそのものの生成

前処理の方法、データ拡張戦略、さらには学習環境そのものをメタ学習の対象とする手法が多数提案されています [191, 306]。

9.3.2.1 モデルパラメータの初期値としてのメタ知識の学習

同時訓練の問題点と解決策

同時訓練の問題

各タスクのサポート集合$D^{\text{tr}}$に対する期待損失の最小化によってメタ知識を学習しようとしている点にある。

重要な課題

(9.21)のような仮説評価時のリスクであるクエリ集合$D^{\text{val}}$に対するリスクを最小化することが重要
この点を考慮したモデルパラメータの初期値に対するメタ学習の成功例が必要

単純な同時訓練では、サポート集合での損失のみを考慮するため、未知のタスクに対する汎化性能が不十分になる可能性があります。

例9.2：正弦関数の同時訓練

設定

タスク$\mathcal{T}$のデータ生成分布$P_{X,Y}^{\mathcal{T}}$：入力$x$が1次元の一様分布$U([-5, 5])$
出力$y$が正弦関数$f_{\mathcal{T}}(x) = a \sin(x + b)$に従う
各タスクを特徴付けるパラメータ$a, b$：それぞれ一様分布$U([0.1, 5.0])$、$U([0, 2\pi])$に従う確率変数
タスクの損失$\mathcal{L}^{\mathcal{T}}$を$\ell_2$損失関数で定義

損失関数：

$$\mathcal{L}^{\mathcal{T}}(x, f_{\mathcal{T}}(x); \theta) = \int_{-5}^5 \|h(x; \theta) - f_{\mathcal{T}}(x)\|^2 dx$$

問題点

期待リスク$\mathbb{E}_{\mathcal{T}}[\mathcal{L}^{\mathcal{T}}]$は恒等的に0を返す仮説$h(x; \theta) \equiv 0$によって最小化されるが、これは明らかに未知のタスクに対する初期値として有用ではない。

MAML（Model-Agnostic Meta-Learning）

MAMLの特徴

Model-agnostic：モデルに対して勾配法によって更新可能であること（微分可能であること）以外を仮定せず
Task-agnostic：回帰、分類または強化学習などのタスクを問わずに適用可能な柔軟性の高いメタ学習手法

MAMLの目標

新たなタスクに対して、少数ショット学習でそれぞれの最適なモデルパラメータが発見できるような共通の初期値を見つけることを目標とします。

図9.3 MAMLのイメージ

新たなタスクの最適なモデルパラメータ$\theta_1^*, \theta_2^*, \theta_3^*$に対して、それぞれを少数ショット学習で到達できるような共通の初期値$\theta$を見つけるためのメタ学習手法です。

MAMLアルゴリズム

MAMLは非常にシンプルで、以下の3ステップを繰り返します

Step 1: タスク分布$P(\mathcal{T})$からタスク$\mathcal{T}_i = (\{D_{T_i}^{\text{tr}}, D_{T_i}^{\text{val}}\}, \mathcal{L}^{T_i})$をサンプリング

$D_{T_i}^{\text{val}}$：それぞれタスク$\mathcal{T}_i$のデータ生成分布$P_{X,Y}^{T_i}$からサンプリングされたサポート集合とクエリ集合
$\mathcal{L}^{T_i}$：損失を表します

各ステップでバッチサイズ分のタスクをサンプリングし、それぞれのタスクに対して個別の適応を行います。

Step 2: タスク$\mathcal{T}_i$固有のモデルパラメータ$\theta^{T_i}$を$\theta_0^{T_i} \leftarrow \theta$と初期化し、勾配法で$S$回更新します。

各反復$s = 1, ..., S$の更新則：

$$\theta^{T_i} = \theta_{s-1}^{T_i} - \alpha \nabla_\theta \mathcal{L}^{T_i}(D_{T_i}^{\text{tr}}; \theta_{s-1}^{T_i}) \quad (9.30)$$

Step 3: 各タスクの検証誤差を小さくするようにすべてのタスクで共有する初期化パラメータ$\theta$を更新します。

$$\theta \leftarrow \theta - \beta \nabla_\theta \sum_{\mathcal{T}_i \sim P(\mathcal{T}_i)} \mathcal{L}^{T_i}(D_{T_i}^{\text{val}}, \theta_S^{T_i}) \quad (9.31)$$

ここで、$\beta > 0$は学習率パラメータです。

MAMLの2レベル最適化

重要な理解

MAMLは、すべてのタスクで同じ仮説集合を用いるとき、メタ知識$\omega$としてモデルパラメータ$\theta$をとった2レベル最適化問題(9.21)と解釈することができます。

(9.21)の制約条件と目的関数の対応

2レベル最適化の要素	MAMLでの対応
制約条件	Step2：個別タスクでの適応
目的関数	Step3：メタパラメータの更新

MAMLは損失関数$\mathcal{L}^{\mathcal{T}}$を取り替えることで教師あり学習におけるメタ学習アルゴリズムにも、強化学習におけるメタ学習アルゴリズムにもなります。

MAMLで使用される損失関数の例

回帰問題

平均二乗損失：

$$\mathcal{L}^{\mathcal{T}}(D_{\mathcal{T}}; \theta) = \sum_{(x,y) \in D_{\mathcal{T}}} (h(x; \theta) - y)^2$$

分類問題

2値交差エントロピー損失：

$$\mathcal{L}^{\mathcal{T}}(D_{\mathcal{T}}; \theta) = \sum_{(x,y) \in D_{\mathcal{T}}} [y \log h(x; \theta) + (1-y) \log(1-h(x; \theta))]$$

強化学習の場合：負の期待報酬

$$\mathcal{L}^{\mathcal{T}}(D_{\mathcal{T}}; \theta) = -\mathbb{E}_{s_1 \sim q, a_i \sim \pi_\theta} \left[ \sum_{t=1}^T R(s_t, a_t) \right]$$

マルコフ決定過程（MDP）をタスクとし、方策関数$\pi_\theta$のパラメータ$\theta$の初期値をメタ学習するアルゴリズムが導出できます。

例9.2のような同時訓練では役に立たない初期化が得られてしまう場合でも、MAMLでは未知のタスクに対してよいパラメータの初期化が得られることが期待できます。

MAMLの計算コストと改善

計算コストの課題

S=1の場合のメタ知識の更新(9.31)：

$$\theta \leftarrow \theta - \beta \nabla_\theta \sum_{\mathcal{T}_i \sim P(\mathcal{T}_i)} \mathcal{L}^{T_i}(D_{T_i}^{\text{val}}; \theta - \alpha \nabla_\theta \mathcal{L}^{T_i}(D_{T_i}^{\text{tr}}; \theta)) \quad (9.32)$$

この実行にはパラメータ$\theta$に関するヘッセ行列の計算が要請される
メタ学習フェーズにおけるパラメータ更新に大きな計算コストがかかる

FOMAML（First-order MAML）

FOMAMLの改善点

Finn等[96]は勾配を1次近似してメタ学習フェーズのパラメータ更新を行う方法（first order MAML (FOMAML)）も提案しています。

FOMAMLの利点

ベース学習フェーズの勾配を保存しておく必要がなく、通常のMAMLに比べて処理が軽量化されています
ヘッセ行列の計算を回避
メモリ使用量の削減

9.3.2.2 オプティマイザとしてのメタ知識の学習

オプティマイザをメタ知識とする動機

従来のアプローチ vs メタ学習アプローチ

従来：モメンタム付きSGDやAdam等の既存の最適化器を利用
メタ学習：$\theta$や損失関数のパラメータに関する勾配$\nabla_\theta \mathcal{L}$などの最適化問題における状態を入力とし、ベース学習の反復ごとにとるべき更新則を生成する関数（最適化アルゴリズムそのもの）を学習

メタ知識$\omega$の範囲

ステップサイズのような単純なハイパーパラメータ [15, 181]
前処理の方法 [221]
複雑な非線形変換としての新たな勾配ベースのオプティマイザ構成 [31, 177, 238, 315]

このアプローチにおけるメタ知識$\omega$は、ステップサイズのような単純なハイパーパラメータから、前処理の方法に至るまで多岐にわたります。

勾配法アルゴリズムの学習

標準的な勾配更新則（式9.33）

$$\theta_{t+1} \leftarrow \theta_t - \alpha_t g_t$$

ここで、$g_t$はパラメータの更新方向を表すベクトルで、素朴な勾配法では$g_t = \nabla_\theta f(\theta_t)$とします。

既存最適化アルゴリズムの例

モメンタム法

$g_0 = 0$として：

$$g_{t+1} = \mu g_t - (1-\mu)\alpha_t \frac{1}{|D_t|} \sum_{(x,y) \in D_t} \nabla_\theta \mathcal{L}(x,y; \theta_t)$$ $$\theta_{t+1} \leftarrow \theta_t + g_{t+1}$$

Adam

$m_0 = v_0 = 0$として：

$$m_{t+1} = \beta_1 m_t + (1-\beta_1)g_t, \quad \hat{m}_{t+1} = \frac{m_{t+1}}{1-\beta_1^t}$$ $$v_{t+1} = \beta_2 v_t + (1-\beta_2)g_t^2, \quad \hat{v}_{t+1} = \frac{v_{t+1}}{1-\beta_2^t}$$ $$\theta_{t+1} \leftarrow \theta_t - \frac{\alpha}{\sqrt{\hat{v}_{t+1}} + \varepsilon} \hat{m}_{t+1}$$

$\mu \in [0,1)$はモメンタム係数と呼ばれ、次の更新方向を決める際に過去の更新方向$g_t$をどれくらい重視するかを制御するパラメータです。

No Free Lunch定理との関係

Wolpertら[318]のNo Free Lunch定理

組合せ最適化問題の設定において、すべての最適化問題に対してランダムサーチよりよい性能を示す最適化アルゴリズムは存在しないことを示しました。

定理の含意

ある最適化アルゴリズムが特定の最適化問題に対してランダムサーチよりよい性能を示すならば、それ以外の最適化問題に対してはランダムサーチより悪い性能を示さなければならない
どんな最適化アルゴリズムも、すべての最適化問題に対する性能を平均するとランダムサーチと同等の性能となってしまう

重要な示唆

一般に最適化アルゴリズムの性能を向上させるためには、問題のサブクラスに特化させることが唯一の方法であることを示唆しています。

Andrychowiczらの手法

勾配法の更新則の一般化（式9.36）

$$\theta_{t+1} \leftarrow \theta_t + g_t(\nabla f(\theta_t); \omega)$$

現在の勾配$\nabla f(\theta_t)$を入力し、その反復における更新量を出力する写像$g_t(f(\theta_t); \omega)$のパラメータ$\omega$を学習するメタ学習問題を考察しました。

$\omega$の意味

(9.34)や(9.35)でモデルパラメータの更新方向と更新量を規定するハイパーパラメータたちを表すもの
タスクのクラスごとによいオプティマイザを人間が設計するのではなく、データから学習させてしまおうという発想

ただし、オプティマイザを学習対象とするアプローチ自体には歴史があり、例えばBengioら[34, 35]による進化計算に基づく更新則の学習法の提案などにそのルーツがあると考えることができます。

メタ期待リスクの新しい定式化

メタ期待リスク（式9.37）

$$\mathcal{R}(\omega) = \mathbb{E}_{f \sim P(f)}[f(\theta^*(\omega))]$$

各$f$が一つのタスクを、$P(f)$がタスク分布を表現している。

問題点

(9.37)のメタ期待リスク$\mathcal{R}(\omega)$は最終時点のパラメータ値$\theta^*$のみに依存します。しかし、更新ステップ$g_t$の訓練であることを考えれば、最適化の初期時点からある時点$T$までのすべての解の履歴に依存する目的関数のほうが適していると考えられます。

改良されたメタ期待リスク（式9.38）

$$\tilde{\mathcal{R}}(\omega) = \mathbb{E}_{f \sim P(f)}\left[\sum_{t=1}^T w_t f(\theta_t)\right]$$

各時点$t = 1, ..., T$に対応する適当な重み$w_t \in \mathbb{R}_{\geq 0}$を導入し、新たなメタ期待リスク$\tilde{\mathcal{R}}(\omega)$を定義します。

RNNによる更新ステップの実装

RNNを用いた更新ステップの生成

$\theta$の更新は$\theta_{t+1} \leftarrow \theta_t + g_t$で行われ、更新ステップ$g_t$はRNNの出力として$(g_t, z_{t+1})^T = h_\omega(\nabla_\theta f(\theta_t), z_t)$で潜在表現$z_{t+1}$とともに生成されます。

重みの設定による柔軟性

重み$w_t$を$w_t = \mathbb{1}[t = T]$（最終時点でのみ1）とり、それ以外の時点では0をとるように設定すれば(9.37)のメタ期待リスクを復元します。

この意味で、(9.38)による定式化は(9.37)の自然な拡張とみなすことができます。

図9.4 勾配法の更新ステップ学習のための計算グラフ

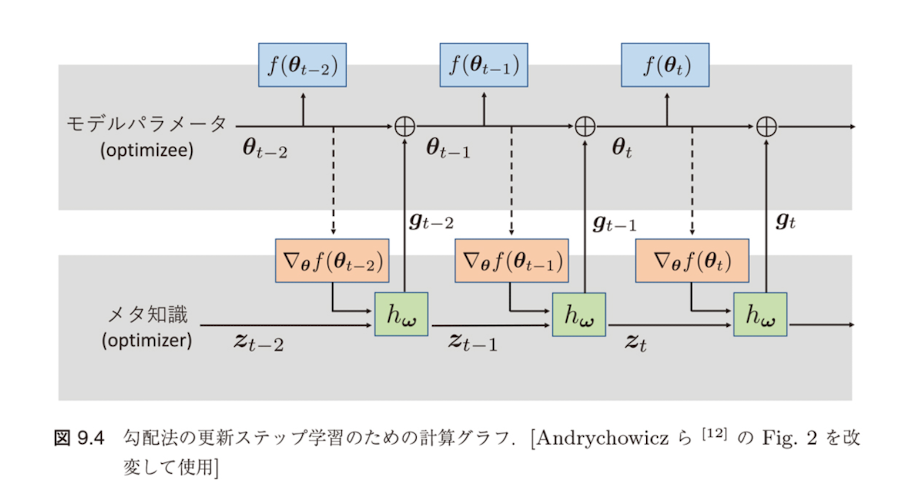
実線に沿った勾配は逆伝播し、破線に沿った勾配は逆伝播しない、すなわち$\partial \nabla_\theta f(\theta_t)/\partial \omega = 0$という仮定をおいています。

計算効率化のための仮定

Andrychowiczら[12]は図の実線に沿った勾配は逆伝播し、破線に沿った勾配は逆伝播しない、すなわち$\partial \nabla_\theta f(\theta_t)/\partial \omega = 0$という仮定をおいています。

仮定の意味

この仮定は、$f$の勾配$\nabla_\theta f(\theta_t)$がメタ知識$\omega$に依存しないことを仮定するものです
この仮定によって$f$のヘッセ行列の計算を回避することができます

この計算効率化は実用上重要ですが、理論的な厳密性とのトレードオフがあります。実際の実装では、この近似が十分な性能を提供することが実験的に確認されています。

RNNオプティマイザの利点

RNNを用いる理由

勾配が過去の更新情報を用いることで効率化できるという経験的な事実に基づいています。

確率的最適化手法との関連

モメンタムやAdam：過去の更新情報を用いて現在の更新方向を補正することによってより高速に最適解まで収束させられることが報告されています
RNNの活用：過去の更新情報を取り入れ、さらにそれをどう現在の更新に反映するかまで含めて学習させられるという点がRNNを用いる最大の理由といえるでしょう

RNNを用いることで、過去の更新情報を取り入れ、さらにそれをどう現在の更新に反映するかまで含めて学習させられるという点が、この手法の最大の利点です。

座標別LSTM最適化

Hochreiterら[132]のRNNアーキテクチャ

全結合型のLSTMでした。しかし、これはモデルパラメータ$\theta$の次元$d$が高いとき、パラメータ数が膨大となり、最適化が不安定になるうえにRNNの計算自体も重くなってしまいます。

Andrychowiczら[12]の改善

$\theta$の成分ごとにLSTM$h_\omega^{(1)}, ..., h_\omega^{(d)}$を用意し、$\theta_1, ..., \theta_d$を個別に最適化するアプローチを提案しています。

利点

$\theta$が高次元の場合でも全結合型LSTMに比べて効率的に最適化を実行することができます
実際に最適化を行う際には、学習を安定させるためにLSTMの入出力を適当に規格化する前処理を各時点で行います

図9.5 座標方向LSTM オプティマイザ

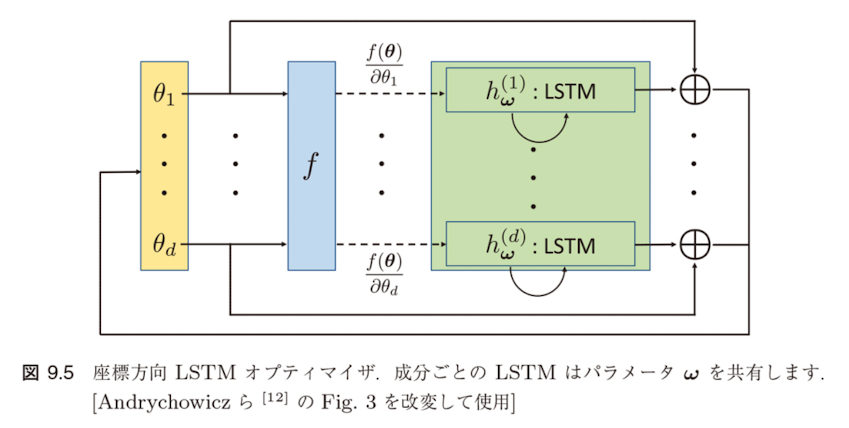
成分ごとのLSTMはパラメータ$\omega$を共有します。

9.3.2.3 Sim2Real転移のためのメタ学習

Sim2Real転移とは

Sim2Real転移（Sim2Real transfer）

シミュレータによって人工的に生成されたデータを訓練データとして用いてさまざまなタスクを解き、そこで得られた知識を実世界のタスクに適用する問題設定を指します。

現在の研究動向

画像認識：主に画像がシミュレータによる人工データとして用いられています
強化学習：セグメンテーションや識別のような画像認識タスクのみでなく、ロボティクスと組み合わせた強化学習タスクが解かれることも多いです
センサー・制御：出力を観測するためのセンサーやアクチュエータの制御など

Sim2Real転移は画像やロボティクスのほか、出力を観測するためのセンサーやアクチュエータの制御、アクションコストが大きいデータを収集するのが困難な分野での重要性が指摘されています。

シミュレーションから実世界への課題

シミュレーションでのギャップ

シミュレーション空間でのモデルの訓練：実世界に比べてもコストが安く、モデルの改善や効率的な訓練が支持されています
実世界への適用時の課題：実世界にはデータやモデルを転移する際に欠陥についても点

主な困難な要因

要因	説明
物理ダイナミクス	重量・摩擦力・接合部の減衰量や弾性係数など
システム同定	system identification
ドメインランダム化	domain randomization による対応

シミュレーションで学習されたモデルが実世界に転移する際の主な課題は、物理的な条件の違いやシステムパラメータの不一致です。

ドメインランダム化に基づくSim2Real転移

ドメインランダム化

ランダムな性質を持つさまざまな類似ドメインを作り、それらすべてで機能するモデルを学習させるアプローチです。実世界の環境がランダムに生成されたようなシミュレーションドメインの中に含まれているならば、学習されたモデルが実世界の環境に適応できる可能性が高いことが期待されます。

基本的なアイデア

実世界の環境がランダムに生成されたシミュレーションドメインに含まれると仮定
多様な環境で汎化性能を持つモデルを学習
実際の環境への適応可能性を高める

このアプローチは、実世界の複雑さと多様性をシミュレーション環境でカバーしようとする試みです。

強化学習でのSim2Real問題設定

強化学習の基本的な問題設定については13.1節を参照してください。

シミュレータの環境を元ドメイン$E_S$
実世界の環境を目標ドメイン$E_T$
モデルの訓練は元ドメインで行う

期待報酬の定式化（式9.39）

$$\mathcal{R}(\theta) = \mathbb{E}_\xi \left[ \mathbb{E}_{\tau \sim p(\tau | \pi_\theta, \xi)} \left[ \sum_{m=1}^M r_m(s_m, a_m, s_{m+1}) \right] \right]$$

記号の意味

元ドメインには$N$個のランダム化パラメータ$\xi = (\xi_1, ..., \xi_N)^T \in \Xi \subset \mathbb{R}^N$がある
$\tau = (s_1, a_1, ..., s_M, a_M, s_{M+1})$は状態$s_m$と行動$a_m$からなるエージェントの学習エピソード
$r_m(s_m, a_m, s_{m+1})$は時点$m$における報酬

ドメインランダム化の実装

ランダム化パラメータの例

環境中に配置されるオブジェクトの形状や位置
色などの条件
強化学習では方策が学習の対象となる

ドメインランダム化の定式化

元ドメインと目標ドメインの不一致度を元ドメインの変動としてモデル化しているものと解釈することができます [227]。

最も簡単な実現方法

一様ドメインランダム化（uniform domain randomization）

各ランダム化パラメータ$\xi_j$を適当な区間$[\xi_j^{\text{low}}, \xi_j^{\text{high}}]$から一様ランダムにサンプリングするというもの [286]。

図9.6 ドメインランダム化によってランダムに生成された学習環境の例

Tobinらの研究によるシーンの外観をドメインランダム化によって多数生成して訓練に用いている例

ランダム化パラメータの具体例

視覚・環境要素

テーブル上のオブジェクトの位置や形、色
オブジェクトの質感
照明の位置や向きなどの条件
シミュレータ内のカメラの位置や向き、視野
画像に加えるランダムノイズの種類と大きさ

物理・動力学要素

物理ダイナミクスのランダム化

実際、Pengら[227]の研究では、ロボット本体の質量や寸法、接合部の減衰量や弾性係数などの条件がランダム化の対象となっています。

OpenAI Roboticsの例

OpenAI Roboticsの成功事例

実際にロボットハンドに50種類の向きを実現させている動画が公開されています。

視覚とダイナミクスの両方でドメインランダム化を適用
継続的な回転制御という複雑なタスクでの成功
50種類の向きという多様な目標状態への対応

この成功例は、適切に設計されたドメインランダム化が実世界の複雑なロボット制御タスクに対して有効であることを実証しています。

一様ドメインランダム化の限界

一様ドメインランダム化の問題点

最も素朴なドメインランダム化の実現方法であり、実際にはより洗練された定式化が望ましいと考えられます。

2レベル最適化問題としての定式化（式9.40）

$$\min_\omega \mathcal{L}(\pi_{\theta^*(\omega)}; E_T)$$

$$\text{subject to } \theta^*(\omega) = \arg\min_\theta \mathbb{E}_{\xi \sim P(\xi; \omega)} [\mathcal{L}(\pi_\theta; E_\xi)]$$

解釈

これは(9.21)のような2レベル最適化問題として実現することができます [301]
$\mathcal{L}(\pi; E)$を環境$E$のもとで方策$\pi$に従って探索を行ったときの損失とするとき、$\xi$の決定問題を$\xi$に従う確率分布$P(\xi; \omega)$のパラメータ$\omega$を推定する問題として書くことができます

ガイド付きドメインランダム化

ガイド付きドメインランダム化の利点

(9.40)の定式化は、タスクの性能や実現境のデータ、シミュレータからのガイダンスなどの補助情報が利用できるという仮定の下でより洗練されたランダム化の戦略を考える方針になります。この意味で、後者をガイド付きドメインランダム化（guided domain randomization）と呼びます。

学習フロー

ガイド付きドメインランダム化では、まず異なるランダム化パラメータ$\xi \sim P(\xi; \omega)$によるそれぞれの環境で方策を学習します。

その後、学習した各方策を目標ドメインの下流タスク（すなわち現実のロボット制御や検証データの予測）で評価しフィードバックを収集します。

得られたフィードバックは用いたランダム化パラメータ$\xi$の良さを評価したものであり、メタ知識$\omega$を更新する際に利用します。

Ruizらの手法

Ruizら[246]の強化学習アプローチ

強化学習における報酬をタスクからのフィードバックと捉え、分布$P(\xi; \omega)$を近似する方策$\pi_\phi$を学習するメタ強化学習のアプローチを提案しました。

記号の簡単のため各下流タスクの報酬を単に$R(\xi)$とおくと、$\pi_\phi$の最適化問題は：

$$\max_\phi R(\phi) = \mathbb{E}_{\xi \sim \pi_\phi} [R(\xi)] \quad (9.41)$$

REINFORCE rule[317]による勾配計算（式9.42）

$$\nabla_\phi R(\phi) = \mathbb{E}_{\xi \sim \pi_\phi} [\nabla_\phi \log(\pi_\phi) R(\xi)]$$

$\nabla_\phi R(\phi)$の不偏推定量は、$K$個のランダム化パラメータのサンプル$\xi_1, ..., \xi_K$を用いて：

$$\frac{1}{K} \sum_{k=1}^K \nabla_\phi \log(\pi_\phi) A_k \quad (9.43)$$

ここで、$A_k = R(\xi_k) - b$はベースライン値$b$からの改善量の推定値であり、$b$には例えば過去の報酬の指数移動平均を用いることができます。

シミュレーションのための学習アルゴリズム

Learning to simulate アルゴリズム

Ruizら[246]による「シミュレーションのための学習」アルゴリズムは以下の手順の繰り返しで構成されます：

Step 1: メタ方策$\pi_\phi$から$K$個のランダム化パラメータ$\xi_k$を生成します。

Step 2: 各$\xi_k$に対応した$K$個の学習エピソード$\tau_k$を$p(\tau | \pi_\theta; \xi_k)$から生成し、タスク固有の方策$\pi_\theta$を学習します。

Step 3: 各タスクの報酬$R(\xi_k)$を取得し、改善量$A_k = R(\xi_k) - b$を計算します。

Step 4: (9.43)を用いて勾配法でメタ方策のパラメータ$\phi$を更新します。

図9.7 Ruizら[246]によるシミュレーションのための学習の流れ

メタ方策→シミュレータ→下流タスク→報酬のフィードバックループを示す

9.4 まとめ

第9章のまとめ

本章で扱った内容

メタ学習の基本概念：帰納バイアス学習としてのメタ学習
統計的メタ学習の定式化：複数タスクに共通する最適な仮説集合の発見
実践的手法：MAML、勾配ベース手法、LSTMオプティマイザ
ドメインランダム化：シミュレーションから実世界への転移

メタ学習の歴史と発展

メタ学習の歴史は比較的古く、はじめは帰納バイアス、すなわち機械学習における帰納的な偏見の研究として始まっていました
近年、広範囲な研究の機械学習分野での研究が行われることとなりました
広範囲な分野の学習支援概念が得られるべきメタ知識として認識されるようになり、メタ学習の対象とする問題は飛躍的に増大しています

本章で紹介したメタ学習の問題設定や方法はその一部であり、解介できなかったものの中にも重要な研究が多数存在しています。詳細は、例えばHospedales らのサーベイ論文 [136] やその引用文献を参照してください。

第9章 メタ学習

第9章 目次

第9章の概要

本章で扱う内容

9.1 機械学習における帰納バイアスとその学習

メタ学習とは

メタ学習の特徴

9.1.1 概念学習とバージョン空間

概念学習の基本例

ウォータースポーツの楽しみ方を予測

特徴量（6つの属性）

仮説の数学的表現

記号の意味

概念学習における訓練データの例

特徴の値域

バージョン空間（Version Space）

表9.1のデータに対するバージョン空間の例

仮説集合のサイズ

9.1.2 帰納バイアスとその学習

バージョン空間における問題

学習アルゴリズムの課題

具体例

オッカムの剃刀（Occam's Razor）

回帰問題への適用例

帰納バイアスとは

帰納バイアスの重要性

9.2 統計的メタ学習の定式化

9.2.1 統計的メタ学習への導入

メタ学習の目的と課題

従来のアプローチの限界

Baxterによる統計的メタ学習の提案

従来手法との違い

単一学習問題の定式化（復習）

基本設定

学習の目的

学習アルゴリズムの定式化

経験リスク最小化

9.2.2 統計的メタ学習の定式化

9.2.2.1 メタ期待リスクとメタ経験リスク

タスク分布と環境の設定

タスクの定義

統計的メタ学習の設定

環境（Environment）

タスク分布の具体例

顔認識問題における帰納バイアス学習

メタ期待リスク（Meta-Expected Risk）

メタ期待リスクの解釈

メタ経験リスク（Meta-Empirical Risk）

メタ学習のデータ設定

メタ経験リスクの特徴と課題

メタ経験リスクの性質

メタ学習アルゴリズム

メタリスクの性質と最適化の課題

集合の包含関係と単調性

9.2.2.2 メタ経験リスクによる近似の精度評価

定理9.3：メタ経験リスクの精度保証(目標)

理論的準備：問題設定と仮説集合の制約

問題設定の簡単化と仮定

仮説の制約

仮説集合の許容性

数学的準備：関数集合の定義

関数集合 $\mathcal{H}_\ell$ と $\mathcal{H}_\ell^M$ の定義

$M$ 個の仮説の平均損失関数

関数集合 $\mathcal{G}_\ell^M$ の定義

期待リスクを返す関数集合 $\mathcal{G}^*$ の定義

$H^*$ 関数の定義

関数集合 $\mathcal{G}^*$ の定義

関数集合上の距離尺度

$\mathcal{G}_\ell^M$ 上の距離 $d_{\mathcal{G}_\ell^M}$

$\mathcal{G}^*$ 上の距離 $d_{\mathcal{G}^*}$

被覆数（Covering Number）

定理9.3：メタ経験リスクの精度保証

定理9.3の意義と実用性

歴史的背景と現代的意義

理論的意義

実用上の課題

深層学習モデルへの応用と解釈

現代的な解釈

大規模モデルでの考察

9.2.2.3 メタ訓練とメタテスト

第9章メタ学習

第9章目次

$\mathcal{G}^$ 上の距離 $d_{\mathcal{G}^}$